题目内容
如图，AB是⊙O的直径，点C、D在圆上，∠D=68°，则∠ABC等于考点：圆周角定理
专题：
分析：首先根据圆周角定理可得∠A=68°，∠BCA=90°，再根据三角形内角和定理可得∠ABC的度数．
解答：解：∵∠D=68°，
∴∠A=68°，
∵AB是⊙O的直径，
∴∠BCA=90°，
∴∠CBA=180°-90°-68°=22°．
故答案为：22°．
∴∠A=68°，
∵AB是⊙O的直径，
∴∠BCA=90°，
∴∠CBA=180°-90°-68°=22°．
故答案为：22°．
点评：此题主要考查了圆周角定理，以及三角形内角和定理，关键是掌握：
圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
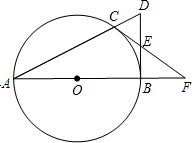如图，点C是以AB为直径的圆O上一点，直线AC与过点B的切线相交于点D，D点E是BD的中点，直线CE交直线AB与点．求证：
已知：AB是⊙O的直径，MN⊥AB，垂足为N，P、Q是
下列运算中，正确的是（ ）
| A、a2+a2=2a4 |
| B、（ab2）2=a2b4 |
| C、a3÷a3=a |
| D、a2•a3=a6 |
将“和谐宜居城市”六个字分别写在一个正方体的六个面上，这个正方体的平面展开图如图，那么在这个正方体中，和“谐”相对的字是（ ）
在平面直角坐标系中，Rt△AOB的位置如图所示，已知∠AOB=90°，AO=BO，点A的坐标为（-3，1）．