Question

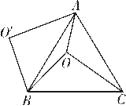
【题目】如图，四边形是正方形，连接，将绕点逆时针旋转得，连接，为的中点，连接，.

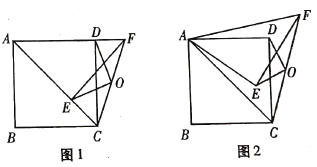
（1）如图1，当时，求证：；

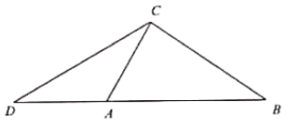
（2）如图2，当时，（1）还成立吗？请说明理由.

Answer 1

【答案】（1）详见解析；（2）当时，成立，理由详见解析.

【解析】

（1）由旋转的性质得：，根据直角三角形斜边中线的性质可得OD=CF，OE=CF，进而可得OD=OE；

（2）连接CE、DF，根据等腰三角形的性质可得，利用角的和差关系可得，利用SAS可证明△ACE≌△AFD，可得CE=DF，∠ECA=∠DFA，利用角的和差关系可得，利用SAS可证明△EOC≌△DOF，即可证明OD=OE，可得（1）结论成立.

（1）∵四边形ABCD是正方形，AC为对角线，

∴∠BAC=45°，

∵将绕点逆时针旋转得，=45°，

∴点E在AC上，

∴，为的中点，

∴

同理：

∴.

（2）当时，成立，理由如下：

连接，如图所示：

∵在正方形中，，AB=AE，

∴，

∵为的中点，

∴，

∵，

∴，

∵=45°，

∴，

∴，

在和中，，

∴，

∴，

∵，

∴，

∴，

在和中，，

∴，

∴.