题目内容
20.(1)已知|a-2017|+|b-2|=0,求a+b的值;(2)已知|a|+|b2+2017|=2017,求a+b的值.
分析 (1)根据非负数的性质列方程求出a、b的值,然后带人代数式进行计算即可得解;
(2)根据平方数非负数和绝对值非负数判断出a、b的值,再相加计算即可得解.
解答 解:(1)由题意得,a-2017=0,b-2=0,
解得a=2017,b=2,
所以,a+b=2017+2=2019;
(2)∵b2≥0,
∴b2+2017≥2017,
又∵|a|+|b2+2017|=2017,
∴a=0,b2+2017=2017,
∴a=0,b=0,
∴a+b=0+0=0.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
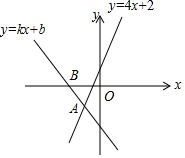 如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式(k-4)x<2-b的解集为x>-1.
如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式(k-4)x<2-b的解集为x>-1.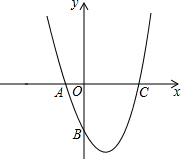 如图,已知抛物线y=(x-1)2+k的图象与x轴交于点A(-1,0),C两点,与y轴交于点B.
如图,已知抛物线y=(x-1)2+k的图象与x轴交于点A(-1,0),C两点,与y轴交于点B.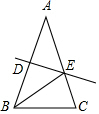 如图,在△ABC中,AB=AC=10cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.若BC=6cm,则△BCE的周长是16 cm.
如图,在△ABC中,AB=AC=10cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.若BC=6cm,则△BCE的周长是16 cm. 如图,在⊙O中,点C在圆周上,∠ACB=45°,则∠AOB=90度.
如图,在⊙O中,点C在圆周上,∠ACB=45°,则∠AOB=90度.