题目内容
8．
如图所示，一皮带轮的坡比是1：2.4，如果将货物从地面用皮带轮送到离地10米的平台，那么该货物经过的路程是26米．
分析 首先根据题意画出图形，根据坡度的定义，由勾股定理即可求得答案．
解答 
解：如图，由题意得：斜坡AB的坡比i=1：2.4，AE=10米，AE⊥BD，
∵i=$\frac{AE}{BE}$=$\frac{1}{2.4}$，
∴BE=24米，
∴在Rt△ABE中，AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=26（米）．
故答案为：26．
点评 此题考查了解直角三角形的应用-坡度坡角问题．此题比较简单，注意掌握数形结合思想的应用，注意理解坡比的定义．
练习册系列答案
相关题目
18．
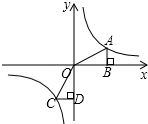如图，A，C是函数$y=\frac{1}{x}$的图象上任意两点，过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记Rt△OAB的面积为S1，Rt△COD的面积S2，则（ ）
如图，A，C是函数$y=\frac{1}{x}$的图象上任意两点，过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记Rt△OAB的面积为S1，Rt△COD的面积S2，则（ ）| A． | S1＞S2 | B． | S1=S2 | C． | S1＜S2 | D． | S1≥S2 |
19．三角形的两边长分别为4和5，第三边长是方程（x-4）（x-1）=0的解，则这个三角形的周长是（ ）
| A． | 10 | B． | 12 | C． | 13 | D． | 10或13 |
如图，在△ABC中，∠1=∠2，∠3=∠4，∠A=65°，则∠F=122.5°．
13．
如图，这个几何体的主视图是（ ）
如图，这个几何体的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
把图分成大小、形状完全相同的两块，且使每块中都含“奋发图强”这4个字，请你试一试，画出分界线．