题目内容
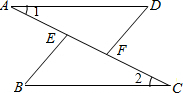 如图,已知点A、E、F、C在同一直线上,∠1=∠2,AE=CF,AD=CB.请你判断BE和DF的关系,并证明你的结论.
如图,已知点A、E、F、C在同一直线上,∠1=∠2,AE=CF,AD=CB.请你判断BE和DF的关系,并证明你的结论.考点:全等三角形的判定与性质
专题:
分析:求出AF=CE,根据SAS证△AFD≌△CEB,推出BE=DF,∠AFD=∠CEB,根据平行线的判定推出即可.
解答:解:BE∥DF,BE=DF,
理由是:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS),
∴BE=DF,∠AFD=∠CEB,
∴BE∥DF.
理由是:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△AFD和△CEB中,
|
∴△AFD≌△CEB(SAS),
∴BE=DF,∠AFD=∠CEB,
∴BE∥DF.
点评:本题考查了平行线的判定和全等三角形的性质和判定的应用.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
下列各组线段,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、5cm,6cm,10cm |
| C、1cm,1cm,3cm |
| D、3cm,4cm,8cm |
 如图,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等.
如图,已知∠AOB及点C、D两点,请利用直尺和圆规作一点P,使得点P到射线OA、OB的距离相等,且P点到点C、D的距离也相等. 已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转90°得到的.(不写作法保留作图痕迹)
已知:如图,四边形ABCD及一点P.求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转90°得到的.(不写作法保留作图痕迹)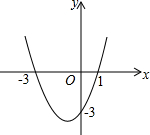 二次函数y=ax2+bx+c(a≠0)的图象如图所示,求:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,求: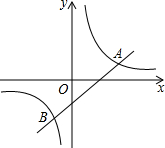 如图,已知反比例函数y=
如图,已知反比例函数y=