题目内容
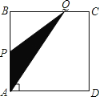
【题目】如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
A.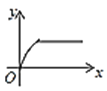 B.
B.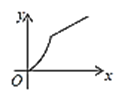 C.
C.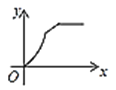 D.
D.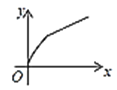
【答案】B
【解析】
根据题意,分两种情况:(1)当动点Q在BC边上运动时;(2)当动点Q在CD边上运动时;然后根据三角形的面积的求法,分类讨论,求出y与x之间的函数关系式,进而判断出y与x之间函数关系图像的是哪个即可.
(1)如图1当动点Q在BC上运动时

∵4÷3=![]() (秒)
(秒)
∴动点Q从点B运动到点C向右的时间是![]() 秒
秒
∵AP=2x,BQ=3x
∴![]()
∴抛物线开口向上.
(2)如图2,当动点Q再CD边上运动时

∵(8+4)÷3=4(秒),![]() (秒)
(秒)
∴动点Q从点C运动到点D需要的时间是![]() 秒
秒
∵AP=2x,BQ=4
∴![]()
综上所述:
故答案选择B.

练习册系列答案
相关题目