题目内容
13.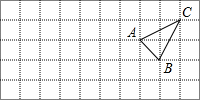 如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,-1)、C(3,1).
如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)、B(2,-1)、C(3,1).(1)请在网格图形中画出平面直角坐标系;
(2)以原点O为位似中心,将△ABC放大2倍,画出放大后的△A′B′C′(画一个即可);
(3)写出△A′B′C′各顶点的坐标:A′(-2,0),B′(-4,2),C′(-6,-2).
分析 (1)利用A,B,C的坐标得出x,y轴的位置;
(2)利用位似图形的性质得出对应点位置进而得出答案;
(3)利用所画图形得出各点坐标.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:△A′B′C′即为所求;
(3)如图所示:A′(-2,0),B′(-4,2),C′(-6,-2).
故答案为:(-2,0),(-4,2),(-6,-2).
点评 此题主要考查了位似变换以及坐标确定位置,利用位似图形的性质得出对应点位置是解题关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
4.下列结论不正确的是( )
| A. | 若a>0,b<0,且a>|b|,则a+b<0 | B. | 若a<0,b>0,且|a|>b,则a+b<0 | ||
| C. | 若a>0,b>0,则a+b>0 | D. | 若a<0,b<0,则a+b<0 |
8.要使分式$\frac{x+3}{(x+3)(x-4)}$有意义,则x应满足( )
| A. | x≠-3 | B. | x≠4 | C. | x≠±3 | D. | x≠-3且x≠4 |
2.某商店在一次买卖中,同时卖出两种货物,每种货物的售价均为960元.若按成本计算,一种货物盈利20%,另一种亏本20%,则这次交易商店( )
| A. | 赚160元 | B. | 赔80元 | C. | 赔240元 | D. | 赚400元 |
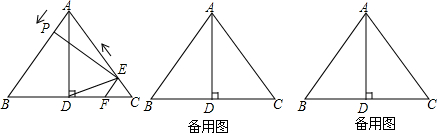
 如图,AD是△ABC的中线,延长AD到E,使DE=AD,连结BE,则有△ACD≌△EBD.
如图,AD是△ABC的中线,延长AD到E,使DE=AD,连结BE,则有△ACD≌△EBD.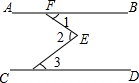 如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.
如图,AB∥CD,∠2=70°,则∠1+∠2+∠3的度数为140°.