题目内容
2.如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.
分析 (1)延长CD交x轴于M,延长BA交x轴于N,则CM⊥x轴,BN⊥x轴,AD∥x轴,BN∥DM,由矩形的性质得出和勾股定理求出BD,BO=15,由平行线得出△ABD∽△NBO,得出比例式$\frac{AB}{BN}=\frac{AD}{NO}=\frac{BD}{BO}=\frac{2}{3}$,求出BN、NO,得出OM、DN、PN,即可得出点D、P的坐标;
(2)当点P在边AB上时,BP=6-t,由三角形的面积公式得出S=$\frac{1}{2}$BP•AD;②当点P在边BC上时,BP=t-6,同理得出S=$\frac{1}{2}$BP•AB;即可得出结果;
(3)设点D(-$\frac{4}{5}$t,$\frac{3}{5}$t);分两种情况:①当点P在边AB上时,P(-$\frac{4}{5}$t-8,$\frac{8}{5}$t),由$\frac{PE}{OE}=\frac{CD}{CB}$和$\frac{PE}{OE}=\frac{CB}{CD}$时;分别求出t的值;
②当点P在边BC上时,P(-14+$\frac{1}{5}$t,$\frac{3}{5}$t+6);由$\frac{PE}{OE}=\frac{CD}{BC}$和$\frac{PE}{OE}=\frac{BC}{CD}$时,分别求出t的值即可.
解答 解:(1)延长CD交x轴于M,延长BA交x轴于N,如图1所示: 则CM⊥x轴,BN⊥x轴,AD∥x轴,BN∥DM,
则CM⊥x轴,BN⊥x轴,AD∥x轴,BN∥DM,
∵四边形ABCD是矩形,
∴∠BAD=90°,CD=AB=6,BC=AD=8,
∴BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
当t=5时,OD=5,
∴BO=15,
∵AD∥NO,
∴△ABD∽△NBO,
∴$\frac{AB}{BN}=\frac{AD}{NO}=\frac{BD}{BO}=\frac{2}{3}$,
即$\frac{6}{BN}=\frac{8}{NO}=\frac{2}{3}$,
∴BN=9,NO=12,
∴OM=12-8=4,DM=9-6=3,PN=9-1=8,
∴D(-4,3),P(-12,8);
(2)如图2所示:当点P在边AB上时,BP=6-t,
∴S=$\frac{1}{2}$BP•AD=$\frac{1}{2}$(6-t)×8=-4t+24; ②当点P在边BC上时,BP=t-6,
②当点P在边BC上时,BP=t-6,
∴S=$\frac{1}{2}$BP•AB=$\frac{1}{2}$(t-6)×6=3t-18;
综上所述:S=$\left\{\begin{array}{l}{-4t+24(0≤t≤6)}\\{3t-18(6<t≤14)}\end{array}\right.$;
(3)设点D(-$\frac{4}{5}$t,$\frac{3}{5}$t);
①当点P在边AB上时,P(-$\frac{4}{5}$t-8,$\frac{8}{5}$t),
若$\frac{PE}{OE}=\frac{CD}{CB}$时,$\frac{\frac{8}{5}t}{\frac{4}{5}t+8}=\frac{6}{8}$,
解得:t=6;
若$\frac{PE}{OE}=\frac{CB}{CD}$时,$\frac{\frac{8}{5}t}{\frac{4}{5}t+8}=\frac{8}{6}$,
解得:t=20(不合题意,舍去);
②当点P在边BC上时,P(-14+$\frac{1}{5}$t,$\frac{3}{5}$t+6),
若$\frac{PE}{OE}=\frac{CD}{BC}$时,$\frac{\frac{3}{5}t+6}{14-\frac{1}{5}t}=\frac{6}{8}$,
解得:t=6;
若$\frac{PE}{OE}=\frac{BC}{CD}$时,$\frac{\frac{3}{5}t+6}{14-\frac{1}{5}t}=\frac{8}{6}$,
解得:t=$\frac{190}{13}$(不合题意,舍去);
综上所述:当t=6时,△PEO与△BCD相似.
点评 本题是四边形综合题目,考查了矩形的性质、勾股定理、相似三角形的判定与性质、三角形面积的计算等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,由三角形相似得出比例式才能得出结果.

| A. | [x]=x(x为整数) | B. | 0≤x-[x]<1 | C. | [x+y]≤[x]+[y] | D. | [n+x]=n+[x](n为整数) |
| A. | 5000条 | B. | 2500条 | C. | 1750条 | D. | 1250条 |
| A. | y=-2(x+1)2 | B. | y=-2(x+1)2+2 | C. | y=-2(x-1)2+2 | D. | y=-2(x-1)2+1 |
 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )| A. | x>-2 | B. | x>0 | C. | x>1 | D. | x<1 |
| A. | -16 | B. | -8 | C. | 8 | D. | 16 |
| A. | ∠BAF=150° | B. | AB=AF | C. | EF=BC | D. | ∠CAF=60° |
 老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.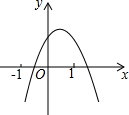 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法正确的个数是( )