题目内容
 如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,当点D落在BC上点D′时,则∠AD′B=
如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,当点D落在BC上点D′时,则∠AD′B=考点:含30度角的直角三角形,旋转的性质
专题:
分析:由条件可得AD′=AD,则可得到
=
,利用特殊角的三角函数值可求得∠AD′B的大小.
| AB |
| AD′ |
| 1 |
| 2 |
解答:解:
∵将AD绕点A顺时针旋转得到AD′,
∴AD′=AD=2,
又四边形ABCD为矩形,
∴∠B=90°,
∴sin∠AD′B=
=
,
∴∠AD′B=30°,
故答案为:30.
∵将AD绕点A顺时针旋转得到AD′,
∴AD′=AD=2,
又四边形ABCD为矩形,
∴∠B=90°,
∴sin∠AD′B=
| AB |
| AD′ |
| 1 |
| 2 |
∴∠AD′B=30°,
故答案为:30.
点评:本题主要考查旋转的性质及特殊角的三角函数值,结合条件求得sin∠AD′B=
=
是解题的关键.注意熟记30°、45°、60°角的三角函数值.
| AB |
| AD′ |
| 1 |
| 2 |

练习册系列答案
相关题目
下列计算错误的是( )
| A、a3•a-2=a | ||
| B、a4÷a3=a2 | ||
| C、a3-3a3=-2a3 | ||
D、(-1+
|
在分式
(a、b为正数)中,a、b的值分别扩大为原来的2倍,则分式的值( )
| a+b |
| a-b |
| A、不变 | ||
B、缩小为原来的
| ||
C、缩小为原来的
| ||
| D、扩大为原来的2倍 |
下列方程变形正确的是( )
A、由
| ||
B、由
| ||
C、由
| ||
D、由
|
 如图所示,∠AOB=90°,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON=
如图所示,∠AOB=90°,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON=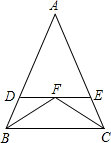 如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E.
如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E. 如图,大圆的半径是R,小圆面积是大圆面积的
如图,大圆的半径是R,小圆面积是大圆面积的