题目内容
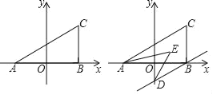
【题目】如图,在平面坐标系中,A(a,0),B(b,0),C(x,y)且满足(a+b)2+|a﹣b﹣4|=0,y=![]() +2.
+2.
(1)求三角形ABC的面积;
(2)若过B作BD∥AC交y轴于D,且AE、DE平分∠CAB、∠ODB,如图,求∠AED的度数;
(3)在y轴上是否存在点P,①使得△ABC和△ACP的面积相等,若存在,求出P点的坐标:若不存在,请说明理由;②若△ACP的面积是△ABC面积的2018倍成立,直接写出P点的坐标;若不存在,请说明理由.
【答案】(1)S△ABC=4;(2)∠AED=45°;(3)存在.①P点坐标为(0,3)或(0,﹣1),②P点坐标为(0,4037)或(0,﹣4035),理由见解析.
【解析】
(1)根据非负数的性质得到a=﹣b,a﹣b+4=0,解得a=﹣2,b=2,再根据y=![]() +2,求出x=2,y=2,则A(﹣2,0),B(2,0),C(2,2),即可计算出三角形ABC的面积=4;
+2,求出x=2,y=2,则A(﹣2,0),B(2,0),C(2,2),即可计算出三角形ABC的面积=4;
(2)由于CB∥y轴,BD∥AC,则∠CAB=∠ABD,即∠3+∠4+∠5+∠6=90°,过E作EF∥AC,则BD∥AC∥EF,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED=∠1+∠2=![]() ×90°=45°;
×90°=45°;
(3)先根据待点系数法确定直线AC的解析式为y=![]() x+1,则G点坐标为(0,1),即可得出PG=|t﹣1|,
x+1,则G点坐标为(0,1),即可得出PG=|t﹣1|,
①利用S△PAC=S△APG+S△CPG=4进行计算,即可得出结论;
②利用S△PAC=S△APG+S△CPG=4×2018进行计算,即可得出结论.
(1)∵(a+b)2+|a﹣b+4|=0,
∴a=﹣b,a﹣b+4=0,
∴a=﹣2,b=2,
∵y=![]() +2,
+2,
∴x=2,y=2,
∴A(﹣2,0),B(2,0),C(2,2)
∴CB⊥AB,
∴S△ABC=![]() ×4×2=4;
×4×2=4;
(2)如图1,∵CB∥y轴,BD∥AC,
∴∠CAB=∠ABD,
∴∠3+∠4+∠5+∠6=90°,
过E作EF∥AC,
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠4=∠1,∠5=∠6=∠2,
∴∠AED=∠1+∠2=![]() ×90°=45°;
×90°=45°;
(3)存在.理由如下:如图2,
设P点坐标为(0,t),直线AC的解析式为y=kx+b,
把A(﹣2,0)、C(2,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=![]() x+1,
x+1,
∴G点坐标为(0,1),
∴PG=|t﹣1|,
①∵△ABC和△ACP的面积相等,
∴S△PAC=S△APG+S△CPG=![]() |t﹣1|×2+
|t﹣1|×2+![]() |t﹣1|×2=4,解得t=3或t=﹣1,
|t﹣1|×2=4,解得t=3或t=﹣1,
∴P点坐标为(0,3)或(0,﹣1),
②∵△ACP的面积是△ABC面积的2018倍,
∴S△PAC=S△APG+S△CPG=![]() |t﹣1|×2+
|t﹣1|×2+![]() |t﹣1|×2=4×2018,解得t=4037或t=﹣4035,
|t﹣1|×2=4×2018,解得t=4037或t=﹣4035,
∴P点坐标为(0,4037)或(0,﹣4035),








