题目内容
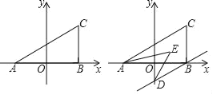
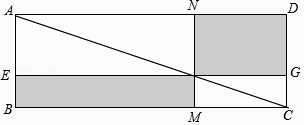
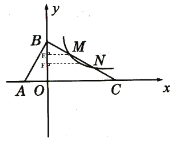
【题目】如图，在平面直角坐标系中，有四边形
，且
，
，
，
．
（1）求证：四边形是矩形；
（2）若反比例函数
与
交于
、
两点，且
，求
的值．
【答案】（1）详见解析；（2）
【解析】
（1）先求出AB，CD，BC，AD，AC的长，再根据勾股定理的逆定理得出∠ABC＝90°，从而判断四边形ABCD是矩形；
（2）作
轴于
，
轴于
，可得
，求出直线BC解析式，设
为
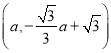，则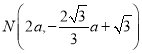
，根据反比例函数图象上点的坐标特征列式求出a的值，得到点M的坐标即可求出k值．
解：（1）∵
，
，
，
，
∴
，
同理可得：
，
，
，
∴四边形
是平行四边形，
∵AC＝3+1＝4，
∴AB2+BC2＝AC2，
∴∠ABC＝90°，
∴四边形是矩形；
（2）作轴于，轴于，则
，
∵
，
∴，
设直线BC解析式为：
，
代入，得：
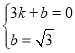，解得：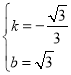
，
∴直线
解析式为：
，
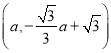设为，则，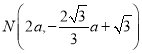
∴
，
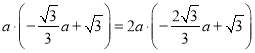解得：
，
∴
，
∴
．
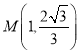练习册系列答案
相关题目
