题目内容
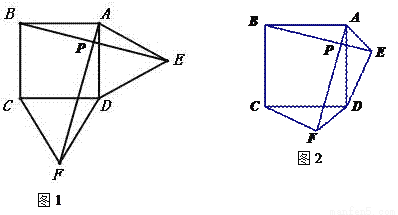
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE,AF,BE相交于点P.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE,AF,BE相交于点P.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明.

 名校课堂系列答案
名校课堂系列答案