题目内容
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(
的图象交于点A(![]() ,n)和B.
,n)和B.
(1)求k的值和点B的坐标;
(2)如果P是x轴上一点,且AP=AB,直接写出点P的坐标
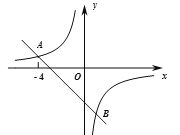
【答案】(1)k=-3,B(1,-4) ;(2)P(3,0)或(-11,0)
【解析】
(1)将点A的坐标带入反比例函数解析式中,求出n值,再将A点的坐标带入一次函数解析式中即可求出k值,联立一次函数解析式与反比例函数解析式成方程组,解方程组即可得出结论;
(2)设出点P的坐标为(m,0).根据两点间的距离公式表示出线段AP和AB的长度,根据AP=AB得出关于m的一元二次方程,解方程即可得出结论.
(1)把A(4,n)代入y=![]() 中,
中,
得:n=![]() =1,
=1,
把A(4,1)代入y=x+k中,
得:1=(4)+k,解得:k=3.
解方程组 ,得
,得![]() .或
.或![]()
∴点B的坐标是(1,4).
(2)设点P的坐标为(m,0).
则:![]() ,
,![]()
∵AP=AB,
∴![]() ,即m
,即m![]() +8m33=0,
+8m33=0,
解得:m![]() =11,m
=11,m![]() =3.
=3.
答:点P的是坐标(3,0)或(11,0).

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
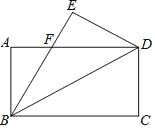
黄冈课堂作业本系列答案【题目】数学活动课上,老师提出问题:如图,有一张长4dm,宽3dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.

下面是探究过程,请补充完整:
(1)设小正方形的边长为x dm,体积为y dm3,根据长方体的体积公式得到y和x的关系式: ;
(2)确定自变量x的取值范围是 ;
(3)列出y与x的几组对应值.
x/dm | … |
|
|
|
|
|
|
|
|
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | m | 3.0 | 2.8 | 2.5 | n | 1.5 | 0.9 | … |
(4)在下面的平面直角坐标系![]() 中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
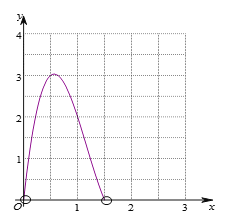
结合画出的函数图象,解决问题:
当小正方形的边长约为 dm时,(保留1位小数),盒子的体积最大,最大值约为 dm3.(保留1位小数)
【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?