题目内容
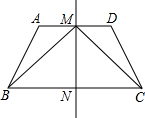 如图,四边形ABCD为轴对称图形,对称轴为直线MN,MN与AD交于点M,与BC交于点N,已知△AMB的周长为62,△BMC的周长为92,四边形ABCD的周长为104,求BM的长.
如图,四边形ABCD为轴对称图形,对称轴为直线MN,MN与AD交于点M,与BC交于点N,已知△AMB的周长为62,△BMC的周长为92,四边形ABCD的周长为104,求BM的长.考点:轴对称的性质
专题:
分析:根据轴对称图形的性质得到AB=CD,BM=CM,AM=DM,BN=CN.所以根据相关图形的周长公式,借助于方程组来求BM的长度即可.
解答:解:∵四边形ABCD为轴对称图形,对称轴为直线MN,
∴设AB=CD=x,BM=CM=y,AM=DM=z,BN=CN=t.
则依题意得:
,则
,
由③得 x+z=52-t,④
把④代入①得 y-t=10,⑤
联立②⑤,解得 y=28.
即BM=28.
∴设AB=CD=x,BM=CM=y,AM=DM=z,BN=CN=t.
则依题意得:
|
|
由③得 x+z=52-t,④
把④代入①得 y-t=10,⑤
联立②⑤,解得 y=28.
即BM=28.
点评:本题考查了轴对称的性质.此题借助于方程来求BM的长度,也可以利用图中相关图形的周长间的关系得到BM的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列四个角度不是正多边形内角的是( )
| A、60° | B、108° |
| C、120° | D、155° |
 某印刷厂有甲、乙两种收费方式,除按所印刷数量收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示.
某印刷厂有甲、乙两种收费方式,除按所印刷数量收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示.