Question

如图，梯形ABCD中，AD∥BC，AB=3，BC=4，连结BD，∠BAD的平分线交BD于 点E，且AE∥CD，则AD的长为（ ）.

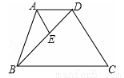
A．1 B．2 C．3 D．4

Answer 1

A.

【解析】

试题分析：延长AE交BC于F，根据角平分线的定义可得∠BAF=∠DAF，由平行的性质可得∠DAF=∠AFB，所以∠BAF=∠AFB，所以AB=BF，即可得到CF=4-3=1，根据平行四边形的判定可得四边形ADCF是平行四边形，所以AD=CF=1.

故选：A.

考点：角平分线的定义；等腰三角形的判定；平行四边形的判定和性质.

考点分析： 考点1：四边形 四边形：四边形的初中数学中考中的重点内容之一，分值一般为10-14分，题型以选择，填空，解答证明或融合在综合题目中为主，难易度为中。主要考察内容：①多边形的内角和，外角和等问题②图形的镶嵌问题③平行四边形，矩形，菱形，正方形，等腰梯形的性质和判定。突破方法：①掌握多边形，四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答，多种情况分析。 试题属性

• 题型：
• 难度：
• 考核：
• 年级：