题目内容
 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )A.16
B.17
C.18
D.19
【答案】分析:由图可得,S1的边长为3,由AC= BC,BC=CE=
BC,BC=CE= CD,可得AC=2CD,CD=2,EC=
CD,可得AC=2CD,CD=2,EC= ;然后,分别算出S1、S2的面积,即可解答.
;然后,分别算出S1、S2的面积,即可解答.
解答: 解:如图,设正方形S2的边长为x,
解:如图,设正方形S2的边长为x,
根据等腰直角三角形的性质知,AC= x,x=
x,x= CD,
CD,
∴AC=2CD,CD= =2,
=2,
∴EC2=22+22,即EC= ;
;
∴S2的面积为EC2= =8;
=8;
∵S1的边长为3,S1的面积为3×3=9,
∴S1+S2=8+9=17.
故选B.
点评:本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.
 BC,BC=CE=
BC,BC=CE= CD,可得AC=2CD,CD=2,EC=
CD,可得AC=2CD,CD=2,EC= ;然后,分别算出S1、S2的面积,即可解答.
;然后,分别算出S1、S2的面积,即可解答.解答:
 解:如图,设正方形S2的边长为x,
解:如图,设正方形S2的边长为x,根据等腰直角三角形的性质知,AC=
 x,x=
x,x= CD,
CD,∴AC=2CD,CD=
 =2,
=2,∴EC2=22+22,即EC=
 ;
;∴S2的面积为EC2=
 =8;
=8;∵S1的边长为3,S1的面积为3×3=9,
∴S1+S2=8+9=17.
故选B.
点评:本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.

练习册系列答案
相关题目
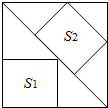 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )| A、16 | B、17 | C、18 | D、19 |
 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为 25、如图:边长为a的大正方形中有一个边长为b的小正方形.
25、如图:边长为a的大正方形中有一个边长为b的小正方形. 如图,边长为a的大正方形是由边长为b的小正方形和四个全等的梯形拼成的,请利用此图证明平方差公式.
如图,边长为a的大正方形是由边长为b的小正方形和四个全等的梯形拼成的,请利用此图证明平方差公式. 如图,边长为a的大正方形内有一个边长为b的小正方形.
如图,边长为a的大正方形内有一个边长为b的小正方形.