题目内容
如图，边长为a的大正方形是由边长为b的小正方形和四个全等的梯形拼成的，请利用此图证明平方差公式．分析：先求出梯形的高为（a-2b），再根据四个梯形的面积列出等式整理即可得证．
解答：证明：∵四个梯形是全等梯形，
∴梯形的高为
，
∴四个梯形的面积=4×
×（a+b）×
=a2-b2，
整理得（a+b）（a-b）=a2-b2．
∴梯形的高为
| a-b |
| 2 |
∴四个梯形的面积=4×
| 1 |
| 2 |
| a-b |
| 2 |
整理得（a+b）（a-b）=a2-b2．
点评：本题考查了平方差公式的几何背景，判断出梯形的高是解题的关键，此类题目通常根据面积相等利用两种方法列出等式求解．
练习册系列答案
相关题目
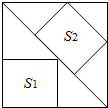如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1+S2的值为
25、如图：边长为a的大正方形中有一个边长为b的小正方形．
如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1+S2的值为（ ）| A、16 | B、17 | C、18 | D、19 |
如图，边长为a的大正方形内有一个边长为b的小正方形．