题目内容
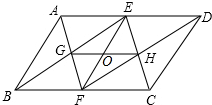 如图已知,平行四边形ABCD中,E、F分别在BC、AD上,AE=BF,AF与BE相交于G,FD和CE相交于点H,求证:
如图已知,平行四边形ABCD中,E、F分别在BC、AD上,AE=BF,AF与BE相交于G,FD和CE相交于点H,求证:(1)GH∥BC;
(2)GH=
| 1 |
| 2 |
考点:平行四边形的判定与性质,三角形中位线定理
专题:证明题
分析:(1)可先证明四边形ABFE是平行四边形,四边形EFCD是平行四边形,进而利用平行四边形的性质得出GH是△BEC的中位线,根据中位线的定理即可得出结论.
(2)根据等量代换即可证得结论;
(2)根据等量代换即可证得结论;
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AE∥CF,AE=CF,
∴四边形ABFE是平行四边形,
∴AF与BE互相平分,
∴G点是BE的中点
同理可证:DE∥CF,DE=CF
∴四边形EFCD是平行四边形,
∴DF与CE互相平分
∴H点是CE的中点
∴GH是△BEC的中位线
∴GH∥BC
∴GH=
BC;
(2)∵AD=BC,GH=
BC,
∴GH=
AD.
∴AD∥BC,AD=BC,
∴AE∥CF,AE=CF,
∴四边形ABFE是平行四边形,
∴AF与BE互相平分,
∴G点是BE的中点
同理可证:DE∥CF,DE=CF
∴四边形EFCD是平行四边形,
∴DF与CE互相平分
∴H点是CE的中点
∴GH是△BEC的中位线
∴GH∥BC
∴GH=
| 1 |
| 2 |
(2)∵AD=BC,GH=
| 1 |
| 2 |
∴GH=
| 1 |
| 2 |
点评:本题主要考查平行四边形的判定和性质,三角形的中位线定理,能够熟练掌握性质和定理是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
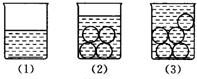 如图是测量一颗玻璃球体积的过程:①将300ml的水倒进一个容量为500ml的杯子中;②将四颗相同的玻璃球放入水中,结果水没有满;③再加一颗同样的玻璃球放入水中,结果水满且溢出.根据以上过程,推测这样一颗玻璃球的体积在( )
如图是测量一颗玻璃球体积的过程:①将300ml的水倒进一个容量为500ml的杯子中;②将四颗相同的玻璃球放入水中,结果水没有满;③再加一颗同样的玻璃球放入水中,结果水满且溢出.根据以上过程,推测这样一颗玻璃球的体积在( )| A、20cm3以上,30cm3以下 |
| B、30cm3以上,40cm3以下 |
| C、40cm3以上,50cm3以下 |
| D、50cm3以上,60cm3以下 |
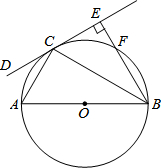 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.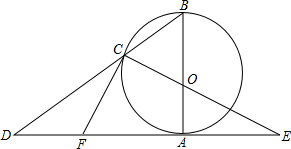 如图,⊙O的直径AB=6cm,DE与⊙O相切于点A,点C为⊙O上的一点,BC的延长线交DE于点D,CO的延长线交DE于点E,过点C作⊙O的切线CF交DE于F,且∠CED的正弦值是方程25x2-15
如图,⊙O的直径AB=6cm,DE与⊙O相切于点A,点C为⊙O上的一点,BC的延长线交DE于点D,CO的延长线交DE于点E,过点C作⊙O的切线CF交DE于F,且∠CED的正弦值是方程25x2-15