Question

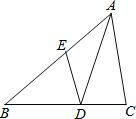
【题目】如图，Rt△ABC中，∠C＝90°，将△ABC沿AB向下翻折后，再绕点A按顺时针方向旋转α度（α＜∠BAC），得到Rt△ADE，其中斜边AE交BC于点F，直角边DE分别交AB，BC于点G，H．

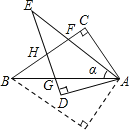
（1）判断∠CAF与∠DAG是否相等，并说明理由．

（2）求证：△ACF≌△ADG．

Answer 1

【答案】（1）∠CAF＝∠DAG．理由见解析；（2）证明见解析.

【解析】

（1）由翻折和旋转的性质，可得∠BAC＝∠EAD，同时减去∠BAE即可得结论；

（2）由翻折和旋转的性质，得到AC＝AD，∠C＝∠D，再加上（1）的结论，可判定全等.

（1）解：∠CAF＝∠DAG．理由如下：

∵Rt△ABC中，∠C＝90°，将△ABC沿AB向下翻折后，再绕点A按顺时针方向旋转α度（α＜∠BAC），得到Rt△ADE，

∴∠BAC＝∠EAD，

∵∠BAC＝∠CAF+∠BAE，∠EAD＝∠DAG+∠BAE，

∴∠CAF＝∠DAG；

（2）证明：∵将△ABC沿AB向下翻折后，再绕点A按顺时针方向旋转α度（α＜∠BAC），得到Rt△ADE，

∴AC＝AD，∠C＝∠D＝90°，

在△ACF和△ADG中，

，

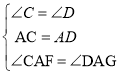∴△ACF≌△ADG（ASA）．