题目内容
如图, 在直角坐标系中,矩形ABCD的边BC在X轴上,点B、D的坐标分别为B(1,0),D(3,3).
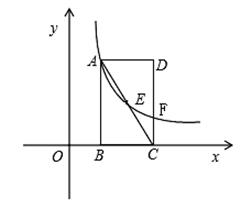
(1)直接写出点C的坐标;
(2)若反比例函数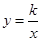 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求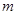 的值及反比例函数的解析式;
的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△CEF,并求出点P的坐标.

(1)直接写出点C的坐标;
(2)若反比例函数
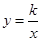 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求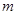 的值及反比例函数的解析式;
的值及反比例函数的解析式;(3)若(2)中的反比例函数的图象与CD相交于点F,连接 EF,在线段AB上(端点除外)找一点P,使得:S△PEF=S△CEF,并求出点P的坐标.
(1)C(3,0)(2)3/2, (3)(1,1)
(3)(1,1)
 (3)(1,1)
(3)(1,1)解:(1)C(3,0)………………………………………(3分)
(2)设直线AC的解析式为 ,则
,则
 ,解得:
,解得:
∴直线AC的解析式为 …………………………………………………(4分)
…………………………………………………(4分)
∵点E(2,m)在直线AC上
∴
∴ ……………………(5分)
……………………(5分)
∵反比例函数y= 的图象经过点E
的图象经过点E
∴
∴反比例函数的解析式为 ……………………………………………………(7分)
……………………………………………………(7分)
(3)在 中,当
中,当 时,
时, ∴
∴ ………………………………(8分)
………………………………(8分)
过点C作直线PC∥EF交AB于P,
则 ………………………(9分)
………………………(9分)
设直线EF的解析式为
∴ 解得:
解得: ∴
∴ ……………(10分)
……………(10分)
设直线PC的解析式为 ,并把C(3,0)代入得:
,并把C(3,0)代入得:
∴ …………………………………………………………………(12分)
…………………………………………………………………(12分)
当 时,y=1 ∴点P(1,1) ………………………………………(13分)
时,y=1 ∴点P(1,1) ………………………………………(13分)
(1)由D点坐标得
(2)求出直线AC的解析式,把E的坐标代入求出m的值,从而求得反比例函数的解析式
(3)过点C作直线PC∥EF交AB于P,求出直线EF的解析式,得出直线PC的解析式,从而求出点P的坐标
(2)设直线AC的解析式为
 ,则
,则 ,解得:
,解得:
∴直线AC的解析式为
 …………………………………………………(4分)
…………………………………………………(4分)∵点E(2,m)在直线AC上
∴

∴
 ……………………(5分)
……………………(5分)∵反比例函数y=
 的图象经过点E
的图象经过点E∴

∴反比例函数的解析式为
 ……………………………………………………(7分)
……………………………………………………(7分)(3)在
 中,当
中,当 时,
时, ∴
∴ ………………………………(8分)
………………………………(8分)过点C作直线PC∥EF交AB于P,

则
 ………………………(9分)
………………………(9分)设直线EF的解析式为

∴
 解得:
解得: ∴
∴ ……………(10分)
……………(10分)设直线PC的解析式为
 ,并把C(3,0)代入得:
,并把C(3,0)代入得:
∴
 …………………………………………………………………(12分)
…………………………………………………………………(12分)当
 时,y=1 ∴点P(1,1) ………………………………………(13分)
时,y=1 ∴点P(1,1) ………………………………………(13分)(1)由D点坐标得
(2)求出直线AC的解析式,把E的坐标代入求出m的值,从而求得反比例函数的解析式
(3)过点C作直线PC∥EF交AB于P,求出直线EF的解析式,得出直线PC的解析式,从而求出点P的坐标

练习册系列答案
相关题目
 交于A、B两点,其横坐标分别为1和5,则不等式k1x<
交于A、B两点,其横坐标分别为1和5,则不等式k1x<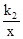 +b的解集是 ▲ .
+b的解集是 ▲ .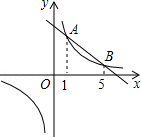
 中,A、B为反比例函数
中,A、B为反比例函数
 的图象上两点,A点的横坐标与B点的纵坐标均为1,将
的图象上两点,A点的横坐标与B点的纵坐标均为1,将 ,B点的对应点为
,B点的对应点为 .
.
 .动点
.动点 从
从 点出发沿线段
点出发沿线段 同时从
同时从 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点 秒,试探究:是否存在使
秒,试探究:是否存在使 为等腰直角三角形的
为等腰直角三角形的 中,菱形
中,菱形 的顶点
的顶点 在
在 轴上,顶点
轴上,顶点 落在反比例函数
落在反比例函数 (
( )的图象上.一次函数
)的图象上.一次函数 (
( )的图象与该反比例函数的图象交于
)的图象与该反比例函数的图象交于 两点,与
两点,与 .已知
.已知 ,
, ,点
,点 ,
, ).
).
 、
、 ,求△
,求△ 的面积.
的面积.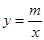 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线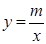 (x>0)和
(x>0)和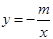 (x<0)于M,N两点.
(x<0)于M,N两点.
 与宽
与宽 之间的函数关系用图象大致可表示为( )
之间的函数关系用图象大致可表示为( )
 的值为 .
的值为 .
 的图象经过点
的图象经过点 ,则此函数的关系是 .
,则此函数的关系是 . 的图象是双曲线, 在每一象限内, y随x增大而增大, 则m的取值为 ( )
的图象是双曲线, 在每一象限内, y随x增大而增大, 则m的取值为 ( )