题目内容
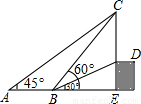
 如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).
如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).分析:设CE=x米,在直角△ACE和直角△BCE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BDE中利用三角函数求得DE的长,则CD的长度即可求解.
解答:解:设CE=x米.在直角△ACE中,∠A=45°,则AE=CE=x米;
在直角△BCE中,BE=
CE=
x米,
∵AB=AE-BE=6米,
则x-
x=6,
解得:x=9+3
.则BE=3
+3米.
在直角△BED中,DE=
BE=
(3
+3)=3+
米.
∴CD=CE-DE=9+3
-(3+
)=6+2
≈9.4(米).
答:电线杆CD的高约是9.4米.
在直角△BCE中,BE=
| ||
| 3 |
| ||
| 3 |
∵AB=AE-BE=6米,
则x-
| ||
| 3 |
解得:x=9+3
| 3 |
| 3 |
在直角△BED中,DE=
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
∴CD=CE-DE=9+3
| 3 |
| 3 |
| 3 |
答:电线杆CD的高约是9.4米.
点评:本题考查了仰角的定义,以及三角函数,正确求得CE的长度是关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
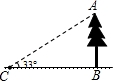 (Ⅰ)如图,从点C测得树的顶端的仰角为33°,BC=20米,则树高AB=
(Ⅰ)如图,从点C测得树的顶端的仰角为33°,BC=20米,则树高AB= 探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=88°,那么∠ABO和∠DCO各是多少度?
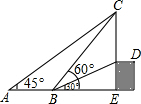
探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关.如图,从点O照射到抛物线上的光线OB,OC等反射以后沿着与POQ平行的方向射出.图中如果∠BOP=45°,∠QOC=88°,那么∠ABO和∠DCO各是多少度?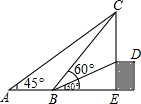 如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).
如图,从点A看一高台上的电线杆CD,顶端C的仰角为45°,向前走6米到B点,测得其顶端C和杆底D的仰角分别是60°和30°,求电线杆CD的高(精确到0.1米).