题目内容
已知在△ABC中,点D、点E分别在边AB和边AC上,且AD=2DB,AE=2EC,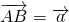 ,
, ,用
,用 、
、 表示向量
表示向量 正确的是
正确的是
- A.

- B.

- C.

- D.

D
分析:首先根据题意画出图形,由AD=2DB,AE=2EC,可得DE∥BC,△ADE∽△ABC,则可知DE= BC,又由
BC,又由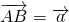 ,
, ,求得
,求得 的值,则问题得解.
的值,则问题得解.
解答: 解:∵AD=2DB,AE=2EC,
解:∵AD=2DB,AE=2EC,
∴ ,
,
∴DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=2:3,
∴DE= BC,
BC,
∵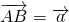 ,
, ,
,
∴ =
= -
- =
= -
- ,
,
∴ =
= (
( -
- )=
)=
 -
-
 .
.
故选D.
点评:此题考查了平面向量的知识以及相似三角形的判定与性质等知识.解此题的关键是根据题意画出图形,利用数形结合思想求解.
分析:首先根据题意画出图形,由AD=2DB,AE=2EC,可得DE∥BC,△ADE∽△ABC,则可知DE=
 BC,又由
BC,又由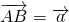 ,
, ,求得
,求得 的值,则问题得解.
的值,则问题得解.解答:
 解:∵AD=2DB,AE=2EC,
解:∵AD=2DB,AE=2EC,∴
 ,
,∴DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=2:3,
∴DE=
 BC,
BC,∵
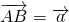 ,
, ,
,∴
 =
= -
- =
= -
- ,
,∴
 =
= (
( -
- )=
)=
 -
-
 .
.故选D.
点评:此题考查了平面向量的知识以及相似三角形的判定与性质等知识.解此题的关键是根据题意画出图形,利用数形结合思想求解.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
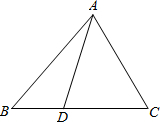 (2012•上海模拟)如图,已知在△ABC中,点D在边BC上,且BD:DC=1:2.如果
(2012•上海模拟)如图,已知在△ABC中,点D在边BC上,且BD:DC=1:2.如果 (2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
(2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( ) 如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.
如图,已知在△ABC中,点D、E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.