题目内容
△ABC的内切圆⊙O与BC，CA，AB分别相切于点D、E、F，且AB=9cm，BC=14cm，CA=13cm，求AF、BD、CE的长．
解：根据切线长定理，设AE=AF=xcm，BF=BD=ycm，CE=CD=zcm．
根据题意，得
，
解，得
．
即AF=4cm、BD=5cm、CE=9cm．
分析：根据切线长定理，可设AE=AF=xcm，BF=BD=ycm，CE=CD=zcm．再根据题意列方程组，即可求解．
点评：此题要熟练运用切线长定理．
注意解方程组的简便方法：三个方程相加，得到x+y+z的值，再进一步用减法求得x，y，z的值．
根据题意，得
，解，得
．即AF=4cm、BD=5cm、CE=9cm．
分析：根据切线长定理，可设AE=AF=xcm，BF=BD=ycm，CE=CD=zcm．再根据题意列方程组，即可求解．
点评：此题要熟练运用切线长定理．
注意解方程组的简便方法：三个方程相加，得到x+y+z的值，再进一步用减法求得x，y，z的值．
练习册系列答案
相关题目
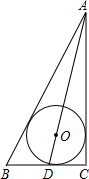如图，⊙O为△ABC的内切圆，∠C=90度，OA的延长线交BC于点D，AC=4，CD=1，则⊙O的半径等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
⊙O是△ABC的内切圆，且∠C=90°，切点为D，E，F，若AF，BE的长是方程x2-13x+30=0的两个根，则S△ABC的值为（ ）
| A、30 | B、15 | C、60 | D、13 |
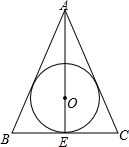如图，等腰△ABC中，AE是底边BC上的高，点O在AE上，⊙O与AB和BC分别相切．
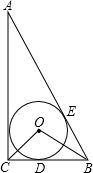（2013•长宁区一模）如图，已知Rt△ABC中，∠ACB=90°，⊙O 是Rt△ABC的内切圆，其半径为1，E、D是切点，∠BOC=105°．求AE的长．