题目内容
如图，BD为半圆O的直径，A为BD延长线上一点，AC切半⊙O于E，BC⊥AC于C，已知BC=5cm，AC=12cm，则⊙O的半径等于| 65 |
| 18 |
| 65 |
| 18 |
分析：连接OE，根据切线性质求出OE⊥AC，推出OE∥BC，得出△AEO∽△ACB，推出比例式，代入求出即可．
解答：解：
连接OE，设⊙O的半径是R，则OE=OB=R，
在Rt△ACB中，由勾股定理得：AB=
=
=13，
∵AC切半圆O于E，
∴OE⊥AC，
∴∠OEA=90°=∠C，
∴OE∥BC，
∴△AEO∽△ACB，
∴
=
，
∴
=
，
R=
，
故答案为：
．
连接OE，设⊙O的半径是R，则OE=OB=R，
在Rt△ACB中，由勾股定理得：AB=
| AC2+BC2 |
| 122+52 |
∵AC切半圆O于E，
∴OE⊥AC，
∴∠OEA=90°=∠C，
∴OE∥BC，
∴△AEO∽△ACB，
∴
| OE |
| BC |
| AO |
| AB |
∴
| R |
| 5 |
| 13-R |
| 13 |
R=
| 65 |
| 18 |
故答案为：
| 65 |
| 18 |
点评：本题考查了勾股定理，切线性质，平行线的性质和判定，相似三角形的性质和判定等知识点的综合运用，用了方程思想．
练习册系列答案
相关题目
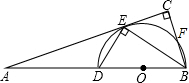已知：如图，BD是半圆O的直径，A是BD延长线上的一点，BC⊥AE，交AE的延长线于点C，交半圆O于点E，且E为
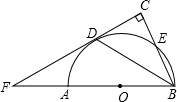C，直线CD交BA的延长线于点F．
如图，BD为半圆O的直径，A为BD延长线上一点，AC切半⊙O于E，BC⊥AC于C，已知BC=5cm，AC=12cm，则⊙O的半径等于________cm．