题目内容
如图，⊙O的两条弦AB、CD相交于点E，连接AC、BD，试证明：AE•BE=CE•DE．
证明：∵∠AEC=∠DEB，∠CAE=∠BDE，
∴△AEC∽△DEB．
∴
．
∴AE•BE=CE•DE．
分析：根据同弧所对的圆周角相等，可证明△AEC∽△DEB，由相似三角形的性质可解．
点评：本题考查了圆周角，相似三角形的判定及性质．
∴△AEC∽△DEB．
∴
．∴AE•BE=CE•DE．
分析：根据同弧所对的圆周角相等，可证明△AEC∽△DEB，由相似三角形的性质可解．
点评：本题考查了圆周角，相似三角形的判定及性质．
练习册系列答案
相关题目
13、已知：如图，⊙O的两条弦AE、BC相交于点D，连接AC、BE．若∠ACB=60°，则下列结论中正确的是（ ）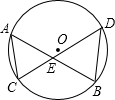
如图，⊙O的两条弦AB、CD相交于点E，连接AC、BD，试证明：AE•BE=CE•DE．
如图，⊙O的两条弦AB、CD相交于E，如果AE=2，EB=6，CE=3，那么CD=
如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O的半径是
如图，⊙O的两条弦AB、CD互相垂直，垂足为点E，且⊙O的半径为2，AB与CD两弦长的平方和等于28，则OE等于（ ）