题目内容
2.对于每个非零自然数n,抛物线y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$与x轴交于An,Bn两点,以An,Bn表示这两点间的距离,则A1B1+A2B2+…+A2013B2013+A2014B2014的值是$\frac{2014}{2015}$.分析 先转换抛物线解析式为两点式:y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$=(x-$\frac{1}{n}$)(x-$\frac{1}{n+1}$),则易求该抛物线与x轴的两个交点坐标;然后根据两点间的坐标差求出距离,找出规律解答即可.
解答 解:y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$=(x-$\frac{1}{n}$)(x-$\frac{1}{n+1}$),
则故抛物线与x轴交点坐标为($\frac{1}{n}$,0)、($\frac{1}{n+1}$,0).
由题意知,AnBn=$\frac{1}{n}$-$\frac{1}{n+1}$,
那么,A1B1+A2B2…+A2013B2013+A2014B2014,
=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{2013}$-$\frac{1}{2014}$)+($\frac{1}{2014}$-$\frac{1}{2015}$),
=1-$\frac{1}{2015}$,
=$\frac{2014}{2015}$,
故答案为$\frac{2014}{2015}$.
点评 题考查的是抛物线与x轴的交点,在解答过程中,注意二次函数与一元二次方程之间的联系,并从中择取有用信息解题;求两点间的距离时,要利用两点间的坐标差来解答.

练习册系列答案
相关题目
17.为了参加市中学生篮球赛,某校一支篮球队购买了10双运动鞋,尺码如下表:
则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码(cm) | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量(双) | 1 | 2 | 3 | 2 | 2 |
| A. | 25.5cm,26cm | B. | 26cm,25.5cm | C. | 25.5cm,25.5cm | D. | 26cm,26cm |
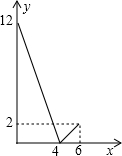 甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.
甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.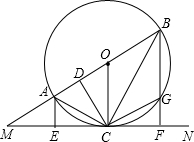 已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.
已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG. 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.