计算(1)$\frac{a}{{{a^2}-4}}+\frac{2}{{4-{a^2}}}$(2)$\frac{x^2}{x-1}+x+1$．题目和参考答案——青夏教育精英家教网—

题目内容

19．计算
（1）$\frac{a}{{{a^2}-4}}+\frac{2}{{4-{a^2}}}$
（2）$\frac{x^2}{x-1}+x+1$．

分析（1）原式变形后，利用同分母分式的减法法则计算即可得到结果；
（2）原式通分并利用同分母分式的加法法则计算即可得到结果．

解答解：（1）原式=$\frac{a}{（a+2）（a-2）}$-$\frac{2}{（a+2）（a-2）}$=$\frac{a-2}{（a-2）（a+2）}$=$\frac{1}{a+2}$；
（2）原式=$\frac{{x}^{2}}{x-1}$+$\frac{{x}^{2}-1}{x-1}$=$\frac{{2{x^2}-1}}{x-1}$．

点评此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

练习册系列答案

人教金学典同步解析与测评学考练系列答案

相关题目

a⁶÷a³=a²

（a²）³=a⁶

10．

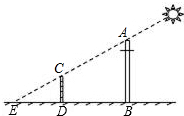小亮希望测量出电线杆AB的高度，他在电线杆旁的点D处立一标杆，标杆的影子DE与电线杆的影子BE部分重叠（即点E、C、A在一直线上），量得DB=2ED米，CD=1.5米．则电线杆AB的高为4.5米．

7．计算或化简
（1）$\sqrt{27}+\left|1\right.-\sqrt{3}\left.{\;}\right|-{（{-1}）^3}$
（2）$\sqrt{32}$-2$\sqrt{2}$+2$\sqrt{0.5}$+$\sqrt{2}×\sqrt{8}$．

14．?ABCD中，∠B=80°，∠C=100°．

4．1-$\sqrt{15}$的值（　　）

11．将正面分别标有数字1，2，3，4的四张质地、大小完全相同的卡片背面朝上放在桌面上．从中随机抽取一张，将抽得的数字作为十位上的数字，然后将所抽取的卡片背面朝上放回并洗匀，再从中随机抽取一张，抽得的数字作为个位上的数字，则组成的两位数大于23的概率是$\frac{9}{16}$．

9．对于二次函数y=x²-（2k+3）x+k²+3k+2，下列表述正确的是（　　）
①函数图象开口向上
②无论k取何值时，函数图象总交于y轴的正半轴
③无论k取何值时，函数图象与x轴的交点间的距离为1
④当k＞$-\frac{3}{2}$时，图象的顶点在第四象限．

试题分类