题目内容
如图，4个正方形的边长均为1，则图中阴影部分三个小扇形的面积和为
- A.
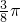
- B.
- C.
- D.
A
分析：根据正方形的性质可得出每个扇形的圆心角的度数，从而阴影部分可看成是圆心角为135°，半径为1是扇形，求解即可．
解答：由观察知三个扇形的半径相等均为1，且左边上下两个扇形的圆心角正好是直角三角形的两个锐角，所以它们的和为90°，右上面扇形圆心角的度数为45°，
∴阴影部分的面积应为：S=
=
π．
故选A．
点评：本题考查了扇形面积的计算及正方形的性质，也考察了学生的观察能力及计算能力，求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．
分析：根据正方形的性质可得出每个扇形的圆心角的度数，从而阴影部分可看成是圆心角为135°，半径为1是扇形，求解即可．
解答：由观察知三个扇形的半径相等均为1，且左边上下两个扇形的圆心角正好是直角三角形的两个锐角，所以它们的和为90°，右上面扇形圆心角的度数为45°，
∴阴影部分的面积应为：S=
=π．故选A．
点评：本题考查了扇形面积的计算及正方形的性质，也考察了学生的观察能力及计算能力，求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
如图，两个正方形的边长均为1，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为
4、如图，两个正方形的边长均为2，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为
如图，4个正方形的边长均为1，则图中阴影部分三个小扇形的面积和为（ ）
如图，两个正方形的边长分别为5与3，两个阴影部分的面积分别为a、b（a＞b），则