题目内容
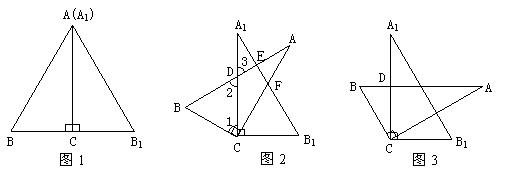
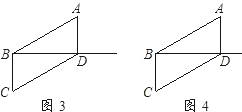
将两块全等的含30º角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30º,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2所示的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①(3分)填空:当旋转角等于20º时,∠BCB1= 度;
②(5分)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)(5分)将图2中的三角板ABC绕点C顺时针方向旋转至图3所示的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.
 |
 |
(1)① 160;………………………………………………………………… 3分
②解:当AB与A1B1垂直时,∠AED=90°,
∴∠3=90°-∠A1=90°-30°=60°,………………………………… 4分
∴∠2=∠3=60°,……………………………………………………… 5分
由已知易得∠B=60°,
∴∠1=180°-∠2-∠B=60°,………………………………………… 6分
∴∠ACA1=30°, ……………………………………………………… 7分
即当旋转角等于30°时,AB与A1B1垂直. ………………………… 8分
(2)∵AB∥CB1,∠ACB1=90°,
∴∠CDB=90°,即CD是△ABC的高, ……………………………… 9分
设BC=![]() ,AC=
,AC=![]() ,则AB=
,则AB=![]() ,A1C=
,A1C=![]() , …………………………… 10分
, …………………………… 10分
∵![]() , …………………………… 11分
, …………………………… 11分
即![]()
∴![]() ,即CD=
,即CD=![]() A1C, ……………………………………… 12分
A1C, ……………………………………… 12分
∴A1D=CD. …………………………………………………………… 13分

练习册系列答案
相关题目
 活用知识,解决问题.
活用知识,解决问题.
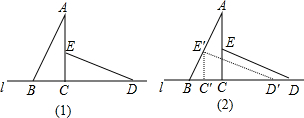 )的位置,使E点落在AB上,则CC′=( )
)的位置,使E点落在AB上,则CC′=( )