题目内容
10.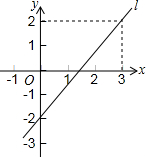 如图所示,直线l是一次函数y=kx+b在直角坐标系内的图象.
如图所示,直线l是一次函数y=kx+b在直角坐标系内的图象.(1)观察图象,试求此一次函数的表达式;
(2)当x=20时,其对应的y的值是多少?
(3)y的值随x值的增大怎样变化?
分析 (1)观察函数的图象,得出一次函数经过点(3,2),(0,-2),代入函数解析式即得出一次函数的表达式;
(2)令x=20,即可得出对应的y的值;
(3)根据一次函数的增减性即可求解.
解答 解:(1)观察图象可得一次函数的图象经过点(3,2),(0,-2),
代入函数的解析式y=kx+b中,得$\left\{\begin{array}{l}{3k+b=2}\\{b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-2}\end{array}\right.$,
所以一次函数的表达式为y=$\frac{4}{3}$x-2;
(2)令x=20,得y=$\frac{4}{3}$×20-2=$\frac{74}{3}$;
(3)∵y=$\frac{4}{3}$x-2,k=$\frac{4}{3}$>0,
∴y的值随x值的增大而增大.
点评 本题考查了利用待定系数法求一次函数的解析式,知道自变量求函数值的方法以及一次函数的增减性.正确求出一次函数的表达式是解题的关键.

练习册系列答案
相关题目
1.已知△ABC中,AB=5,AC=10,BC=2a-1,则a的取值范围是( )
| A. | 2<a<7 | B. | 0<a<8 | C. | 3<a<8 | D. | 12<a<32 |
18.下列变形正确的是( )
| A. | a2-2a-1=a2-(2a-1) | B. | a-b+c-d=a-(b-c+d) | ||
| C. | -x3-x2+2x=+(2x-x2+x3) | D. | -a+b-c+d=-(a-b)-(c+d) |
 如图是屋顶的“人字形“钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为中柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=5m.
如图是屋顶的“人字形“钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为中柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=5m.