题目内容
14.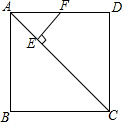 如图,正方形ABCD的边长为1,AC为其对角线,点E为AC上一点且满足CE=CD,过点E作EF⊥AC交AD于点F,则DF的长度为$\sqrt{2}$-1.
如图,正方形ABCD的边长为1,AC为其对角线,点E为AC上一点且满足CE=CD,过点E作EF⊥AC交AD于点F,则DF的长度为$\sqrt{2}$-1.
分析 连接FC,证明Rt△EFC≌Rt△DFC得:EF=FD,由勾股定理求出AC=$\sqrt{2}$,设DF=x,在Rt△AEF中,根据勾股定理列方程:(1-x)2=($\sqrt{2}$-1)2+x2,求出x的值即可.
解答 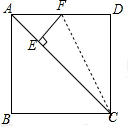 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC=1,
由勾股定理得:AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{2}$,
∵CE=CD=1,
∴AE=AC-CE=$\sqrt{2}$-1,
设DF=x,
连接CF,
∵EF⊥AC,
∴∠FEC=90°,
在Rt△EFC和Rt△DFC中,
∵$\left\{\begin{array}{l}{FC=FC}\\{EC=DC}\end{array}\right.$,
∴Rt△EFC≌Rt△DFC(HL),
∴EF=FD=x,
∴AF=AD-DF=1-x,
在Rt△AEF中,∵AF2=AE2+EF2,
∴(1-x)2=($\sqrt{2}$-1)2+x2,
x=$\sqrt{2}$-1,
∴DF=$\sqrt{2}$-1.
点评 本题考查了正方形的性质,熟知正方形的各角为直角,各边相等是关键;在正方形的题中,可以设所求边长为x,利用勾股定理列方程求解.

练习册系列答案
相关题目
6.下列计算结果正确的是( )
| A. | a3•a3=a9 | B. | (-y)5÷(-y)3=y2 | C. | (a3)2=a5 | D. | (a+b)2=a2+b2 |
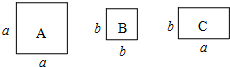 有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(a+2b)的大长方形,则需要C类卡片5张.
有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(a+2b)的大长方形,则需要C类卡片5张.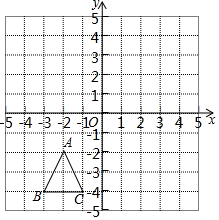 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3),
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3),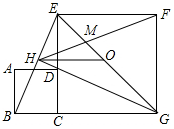 如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论: