题目内容
18．如图，每一幅图中均含有若干个正方形，第①幅图中含有1个正方形；第②幅图中含有5个正方形；…按这样的规律下去，则第⑥幅图中含有91个正方形．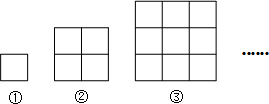
分析 观察图形发现第一个有1个正方形，第二个有1+4=5个正方形，第三个有1+4+9=14个正方形，…第n个有：1+4+9+…+n2=$\frac{1}{6}$n（n+1）（2n+1）个正方形，从而得到答案．
解答 解：观察图形发现第一个有1个正方形，
第二个有1+4=5个正方形，
第三个有1+4+9=14个正方形，
…
第n个有：1+4+9+…+n2=$\frac{1}{6}$n（n+1）（2n+1）个正方形，
第6个有1+4+9+16+25+36=91个正方形，
故答案为：91．
点评 此题考查了图形的变化规律，解题的关键是仔细关系图形并找到规律，利用规律解决问题．
练习册系列答案
相关题目
8．下列给出的方程中，是二元一次方程的是（ ）
| A． | xy=5 | B． | 6x=5y | C． | x+$\frac{1}{y}$=6 | D． | 4x+y2=6 |
10．一抛物线和抛物线y=-2x2的形状、开口方向完全相同，顶点坐标是（-1，3），则该抛物线的解析式为（ ）
| A． | y=-2（x-1）2+3 | B． | y=-2（x+1）2+3 | C． | y=-（2x+1）2+3 | D． | y=-（2x-1）2+3 |
已知：如图所示，AB∥CD，∠A=∠F，∠D=∠E．求证：AF⊥DE．