题目内容
3.在盒子里放有三张分别写有整式a-3、a+1、2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{4}$ |
分析 列举出所有情况,看能组成分式的情况占所有情况的多少即为所求的概率.
解答 解:分母含有字母的式子是分式,整式a-3,a+1,2中,抽到a-3,a+1做分母时组成的都是分式,共有3×2=6种情况,其中a-3,a+1为分母的情况有4种,所以能组成分式的概率=$\frac{4}{6}$=$\frac{2}{3}$.
故选B.
点评 此题考查了列表法与树状图法,用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
相关题目
13.时钟钟面上的分针的长为1,经过30分,分针在钟面上扫过的面积是( )
| A. | $\frac{1}{2}π$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
14.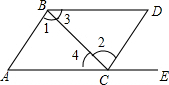 如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )
 如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中能判断AC∥BD的是( )| A. | ∠1=∠2 | B. | ∠D+∠ABD=180° | C. | ∠3=∠4 | D. | ∠DCE=∠A |
8.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成5个三角形,那么这个多边形有( ) 条对角线.
| A. | 13 | B. | 14 | C. | 15 | D. | 5 |
12. 如图,△ABC≌△DEF,则∠E的度数为( )
如图,△ABC≌△DEF,则∠E的度数为( )
 如图,△ABC≌△DEF,则∠E的度数为( )
如图,△ABC≌△DEF,则∠E的度数为( )| A. | 80° | B. | 40° | C. | 62° | D. | 38° |
13.点P位于x轴上方,距x轴4个单位长度,又在y轴左方,距y轴3个单位长度,则点P的坐标是( )
| A. | (3,-4) | B. | (-3,4) | C. | (4,-3) | D. | (-4,3) |