题目内容
问题提出
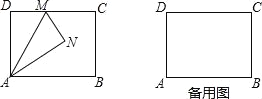
(1)如图①，在△ABC中，∠A＝120°，AB＝AC＝5，则△ABC的外接圆半径R的值为 ．
问题探究
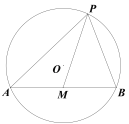
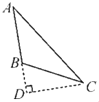
(2)如图②，⊙O的半径为13，弦AB＝24，M是AB的中点，P是⊙O上一动点，求PM的最大值．
问题解决
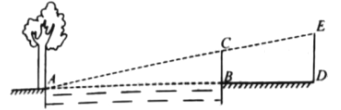
(3)如图③所示，AB、AC、BC是某新区的三条规划路其中，AB＝6km，AC＝3km，∠BAC＝60°，BC所对的圆心角为60°．新区管委会想在BC路边建物资总站点P，在AB、AC路边分别建物资分站点E、F．也就是，分别在
、线段AB和AC上选取点P、E、F．由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷环保和节约成本要使得线段PE、EF、FP之和最短，试求PE＋EF＋FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计)．
图① 图② 图③
练习册系列答案
名校课堂系列答案
相关题目
某校八年级为了了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上的发言次数进行了统计,其结果如下表,并绘制了如图所示两幅不完整的统计图.已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
组别 | 发言次数n |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
发言人数直方图 发言人数扇形统计图
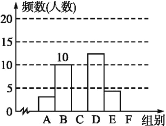
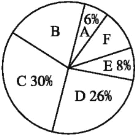
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位男生,E组发言的学生中恰有1位女生,现从A组与E组中分别抽一位学生写调查报告.请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
．
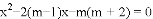