题目内容
19.一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
分析 (1)利用树状图展示所有16种等可能的结果数,然后把它们分别写出来;
(2)利用算术平方根的定义找出大于16小于49的数,然后根据概率公式求解.
解答 解:(1)画树状图:
共有16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;
(2)算术平方根大于4且小于7的结果数为6,
所以算术平方根大于4且小于7的概率=$\frac{6}{16}$=$\frac{3}{8}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果数n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或B的概率.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
10.某机加工车间共有26名工人,现要加工2100个A零件,1200个B零件,已知每人每天加工A零件30个或B零件20个,问怎样分工才能确保同时完成两种零件的加工任务(每人只能加工一种零件)?设安排x人加工A零件,由题意列方程得( )
| A. | $\frac{2100}{30x}$=$\frac{1200}{20(26-x)}$ | B. | $\frac{2100}{x}$=$\frac{1200}{26-x}$ | ||
| C. | $\frac{2100}{20x}$=$\frac{1200}{30(26-x)}$ | D. | $\frac{2100}{x}$×30=$\frac{1200}{26-x}$×20 |
7.学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数$\overline{x}$(单位:分)及方差s2如表所示:
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 7 | 8 | 8 | 7 |
| s2 | 1 | 1.2 | 1 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
14.计算a10÷a2(a≠0)的结果是( )
| A. | a5 | B. | a-5 | C. | a8 | D. | a-8 |
4.一元二次方程2x2-3x+1=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
8.不等式$\frac{x+1}{2}$>$\frac{2x+2}{3}$-1的正整数解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.一组数据5,4,2,5,6的中位数是( )
| A. | 5 | B. | 4 | C. | 2 | D. | 6 |
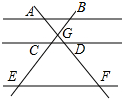 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$.
如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$.