Question

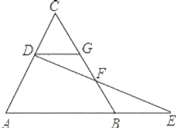
【题目】如图，已知△ABC是等边三角形，D为AC边上的一点，DG∥AB，延长AB到E，使BE=GD，连接DE交BC于F．

(1)求证：GF=BF；

(2)若△ABC的边长为a，BE的长为b，且a，b满足(a﹣7)2+(b﹣3)2=0，求BF的长．

Answer 1

【答案】⑴见解析；⑵BF=2.

【解析】

（1）由得，又，根据三角形全等的判定定理得，再根据三角形全等的性质即得证；

（2）先求出a和b的值，从而可以得BC和DG的长，又得，加上得是等边三角形，则，可知BG的长，再根据，求解即可得.

（1）

（两直线平行，内错角相等）

在和中，

；

（2）由平方数的非负性得

则，即

是等边三角形

又

（两直线平行，同位角相等）

是等边三角形，则

由题（1）的结论可知：

故BF的长为2.