��Ŀ����
����Ŀ����ͼ��ʾ����ABC�У���B=90�㣬AB=6cm��BC=8cm��
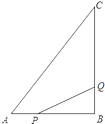
��1���� P�ӵ�A��ʼ��AB����B��1cm/s���ٶ��ƶ�����Q��B�㿪ʼ��BC�����C��2cm/s���ٶ��ƶ������P��Q�ֱ��A��Bͬʱ�������߶�PQ�ܷ���ABC�ֳ������ȵ������֣����ܣ�����˶�ʱ�䣻������˵�����ɣ�
��2����P��������AB�����A�������1cm/s���ٶ��ƶ����� Q������ CB�����C�������2cm/s���ٶ��ƶ���P��Qͬʱ�������ʼ������PBQ�����Ϊ1cm2��
���𰸡���1�����ܣ���2��5��![]() �롢5���5+
�롢5���5+![]() ��.
��.
��������
(1)�辭��x�룬�߶�PQ�ܽ���ABC�ֳ������ȵ������֣��г�������⼴�ɣ�
(2)������������ٵ�P���߶�AB�ϣ���Q���߶�CB�ϣ�0��t��4�����ڵ�P���߶�AB�ϣ���Q���߶�CB���ӳ�������4��t��6��������P���߶�AB���ӳ����ϣ���Q���߶�CB���ӳ�������t>6�����������ۼ������.
�⣺��1���辭��x�룬�߶�PQ�ܽ���ABC�ֳ������ȵ�������
������֪��AP=x��BQ=2x����BP=6��x��
�� ![]() (6��x)2x=
(6��x)2x=![]() ��
��![]() ��6��8��
��6��8��
��x2��6x+12=0��
��b2��4ac��0��
�˷����⣬
���߶�PQ���ܽ���ABC�ֳ������ȵ������֣�
��2����t���PBQ�����Ϊ1��������������ۣ�
�ٵ���P���߶�AB�ϣ���Q���߶�CB��ʱ����ʱ0��t��4��
������֪��![]() (6��t)(8��2t)=1�������ã�t2��10t+23=0����ã�t1=5+
(6��t)(8��2t)=1�������ã�t2��10t+23=0����ã�t1=5+![]() ���������⣬Ӧ��ȥ����t2=5��
���������⣬Ӧ��ȥ����t2=5��![]() ��
��
�ڵ���P���߶�AB�ϣ���Q���߶�CB���ӳ�����ʱ����ʱ4��t��6��������֪��![]() (6��t)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=t2=5��
(6��t)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=t2=5��
�۵���P���߶�AB���ӳ����ϣ���Q���߶�CB���ӳ�����ʱ����ʱt��6��������֪�� ![]() (t��6)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=5+
(t��6)(2t��8)=1�������ã�t2��10t+25=0����ã�t1=5+![]() ��t2=5-
��t2=5-![]() ���������⣬Ӧ��ȥ����
���������⣬Ӧ��ȥ����
��������������5-![]() �롢5���5+
�롢5���5+![]() ���PBQ�����Ϊ1cm2.
���PBQ�����Ϊ1cm2.
�ʴ�Ϊ����1�����ܣ���2��5��![]() �롢5���5+
�롢5���5+![]() ��.
��.

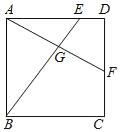
����Ŀ����ͼ��������ABCD�У�E��F�ֱ��ڱ�AD��CD�ϣ�AF��BE�ཻ�ڵ�G����AE=3ED��DF=CF����![]() ��ֵ�ǣ�������
��ֵ�ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
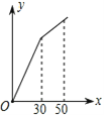
����Ŀ��������ij������ˮ�۸������(����)��(��λ��Ԫ/������)
��ˮ��� | ����ˮ�� | �����ˮ�� |
һ������������ˮ | 0.72 | |
1��һ��һ�� | ||
��һ���ݣ�����ˮ��0��30������/�� | 0.82 | |
�ڶ����ݣ�����ˮ������30������/������ | 1.23 |
�����ˮ�ۺ�ij����������ˮ��x(������)��Ӧ��ˮ��y(Ԫ)�ĺ���ͼ����(����)
A.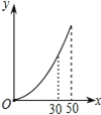 B.
B. C.
C.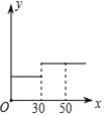 D.
D.