题目内容
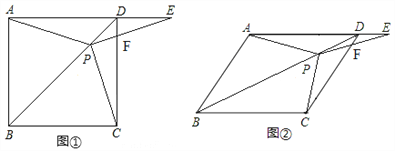
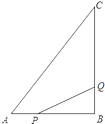
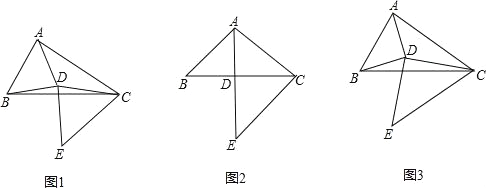
【题目】如图1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=α.
(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3,求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).
【答案】(1)AD+DE=4;(2)①4![]() ;②
;②![]() .
.
【解析】
试题(1)由∠ABC=45°且α=90°,可得到A、D、E三点共线、B、D、C三点共线,故可得AD+DE=4;
(2)①图形见试题解析,设DE与BC相交于点H,连接 AE,交BC于点G,则可证△ADE ≌△BDC,则可得到AE= BC=4,由平移的性质可AE= EF=4,在直角三角形AEF中,由于∠AFE=45°,可以求得AF的长;
②![]() .
.
试题解析:(1) AD+DE=4.
(2)① 补全图形,如下图所示.

设DE与BC相交于点H,连接 AE,交BC于点G,如图.

![]() ∠ADB=∠CDE =90°,∴∠ADE=∠BDC,在 △ADE与△BDC中,∵AD=BD,∠ADE=∠BDC,DE=DC,∴△ADE ≌△BDC,∴AE=" BC" ,∠AED=∠BCD,
∠ADB=∠CDE =90°,∴∠ADE=∠BDC,在 △ADE与△BDC中,∵AD=BD,∠ADE=∠BDC,DE=DC,∴△ADE ≌△BDC,∴AE=" BC" ,∠AED=∠BCD,![]() DE与BC相交于点H,∴∠GHE=∠DHC,∴∠EGH=∠EDC=90°,
DE与BC相交于点H,∴∠GHE=∠DHC,∴∠EGH=∠EDC=90°,![]() 线段CB沿着射线CE的方向平移,得到线段EF,∴EF = CB=4, EF // CB,
线段CB沿着射线CE的方向平移,得到线段EF,∴EF = CB=4, EF // CB,
∴AE= EF,![]() CB//EF,∴∠AEF=∠EGH=90°,
CB//EF,∴∠AEF=∠EGH=90°,![]() AE=EF,∠AEF=90°,∴∠AFE=45°,∴AF=
AE=EF,∠AEF=90°,∴∠AFE=45°,∴AF=![]() =4
=4![]() .
.
②![]() .
.

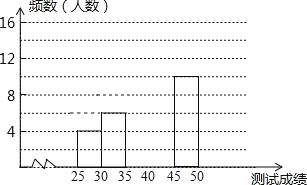
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男生,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,试用列表法或画树状图的方法求小宇和小强两名男同学能分在一组的概率.