题目内容
 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-| 3 |
| 4 |
考点:直角三角形斜边上的中线,一次函数图象上点的坐标特征,勾股定理
专题:
分析:令x=0求出OA的长,令y=0求出OB的长,再利用勾股定理列式求出AB,然后根据直角三角形斜边上的中线等于斜边的一半可得OC=
AB.
| 1 |
| 2 |
解答:解:令x=0则OA=y=6,
令y=0,则-
x+6=0,
解得x=8,
所以,OB=8,
由勾股定理,AB=
=
=10,
∵点C是线段AB的中点,
∴OC=
AB=
×10=5.
故答案为:5.
令y=0,则-
| 3 |
| 4 |
解得x=8,
所以,OB=8,
由勾股定理,AB=
| OA2+OB2 |
| 62+82 |
∵点C是线段AB的中点,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:5.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,一次函数图象上点的坐标特征,勾股定理,熟记性质是解题的关键.

练习册系列答案
相关题目
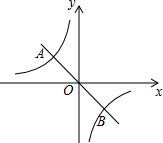 如图正比例函数y=ax的图象与反比例函数y=
如图正比例函数y=ax的图象与反比例函数y= 如图,把一块含45°角的三角形的直角顶点靠在长尺(两边a∥b)的一边b上,若∠1=30°,则三角板的斜边与长尺的另一边a的夹角∠2的度数为
如图,把一块含45°角的三角形的直角顶点靠在长尺(两边a∥b)的一边b上,若∠1=30°,则三角板的斜边与长尺的另一边a的夹角∠2的度数为 如图,在△ABC中,AB的垂直平分线交AC于点E,已知△ABC和△BCE的周长分别是8和5,则AD=
如图,在△ABC中,AB的垂直平分线交AC于点E,已知△ABC和△BCE的周长分别是8和5,则AD=