题目内容
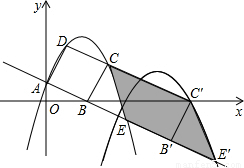
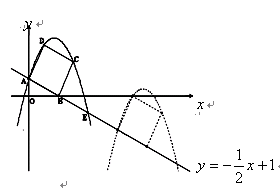
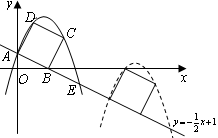
如图,已知直线![]() 交坐标轴于
交坐标轴于![]() 两点,以线段
两点,以线段![]() 为边向上作正方形
为边向上作正方形![]() ,过点
,过点![]() 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为![]() .
.
1.请直接写出点![]() 的坐标
的坐标
2.求抛物线的解析式
3.若正方形以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 下滑,直至顶点
下滑,直至顶点![]() 落在
落在![]() 轴上时停止.设正方形落在
轴上时停止.设正方形落在![]() 轴下方部分的面积为
轴下方部分的面积为![]() ,求
,求![]() 关于滑行时间
关于滑行时间![]() 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量![]() 的取值范围;
的取值范围;
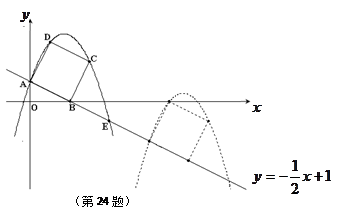
4.在(3)的条件下,抛物线与正方形一起平移,当D落在x轴上时,抛物线与正方形同时停止,求抛物线上![]() 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.
1.![]()
2.![]()
3.当![]() 时,
时,![]() ;
;
当![]() 时,S
时,S![]()
当![]() 时,S=
时,S=![]()
4.15
解析:(1)![]() ;…………………………………………………2分
;…………………………………………………2分
(2)设抛物线为![]() ,抛物线过
,抛物线过![]()
![]() ,
,
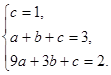 解得
解得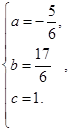 …………………………………………………1分
…………………………………………………1分
∴![]() .……………………………………………………………1分
.……………………………………………………………1分
(3)①当点A运动到点F时,![]()
当![]() 时,如图1,
时,如图1,

∵![]() ,
,![]()
∴![]() ∴
∴![]()
∴![]() ;……2分
;……2分
![]() ②当点
②当点![]() 运动到
运动到![]() 轴上时,
轴上时,![]() ,
,
当![]() 时,如图2,
时,如图2,

![]()
∴![]() ∴
∴![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]() ;…………(2分)
;…………(2分)
③当点![]() 运动到
运动到![]() 轴上时,
轴上时,![]() ,
,
当![]() 时,如图3,
时,如图3,
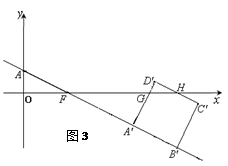
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
![]() ∽
∽![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
=![]() .………(2分)
.………(2分)
(4)∵![]() ,
,![]() ,
,

∴![]() ………………………………………………(1分)
………………………………………………(1分)
=![]()
=![]() .……………………………………………………………(1分)
.……………………………………………………………(1分)

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目

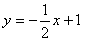 交坐标轴于
交坐标轴于 两点,以线段
两点,以线段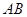 为边向上作正方形
为边向上作正方形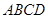 ,过点
,过点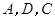 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为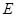 .
.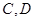 的坐标
的坐标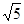 个单位长度的速度沿射线
个单位长度的速度沿射线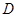 落在
落在 轴上时停止.设正方形落在
轴上时停止.设正方形落在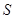 ,求
,求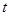 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量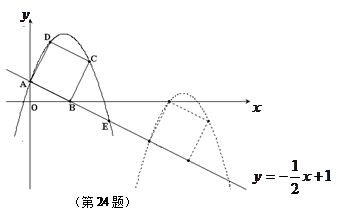
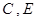 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.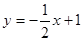 交坐标轴于
交坐标轴于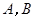 两点,以线段
两点,以线段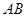 为边向上作正方形
为边向上作正方形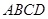 ,过点
,过点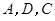 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为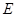 .
.
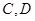 的坐标;
的坐标; 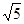 个单位长度的速度沿射线
个单位长度的速度沿射线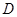 落在x轴上时停止.设正方形落在
落在x轴上时停止.设正方形落在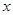 轴下方部分的面积为
轴下方部分的面积为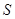 ,求
,求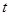 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量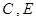 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.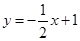 交坐标轴于
交坐标轴于 两点,以线段
两点,以线段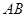 为边向上作正方形
为边向上作正方形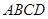 ,过点
,过点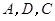 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为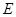 .
.
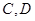 的坐标;
的坐标; 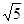 个单位长度的速度沿射线
个单位长度的速度沿射线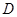 落在
落在 轴上时停止.设正方形落在
轴上时停止.设正方形落在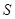 ,求
,求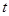 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量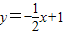 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.