题目内容
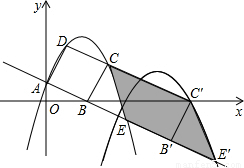
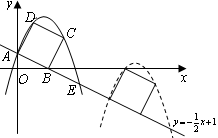
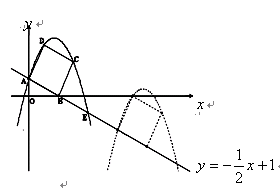
如图,已知直线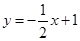 交坐标轴于
交坐标轴于 两点,以线段
两点,以线段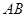 为边向上作正方形
为边向上作正方形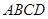 ,过点
,过点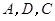 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为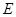 .
.
(1)请直接写出点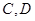 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒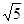 个单位长度的速度沿射线
个单位长度的速度沿射线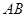 下滑,直至顶点
下滑,直至顶点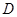 落在
落在 轴上时停止.设正方形落在
轴上时停止.设正方形落在 轴下方部分的面积为
轴下方部分的面积为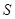 ,求
,求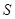 关于滑行时间
关于滑行时间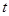 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量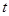 的取值范围;
的取值范围;
(1)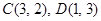 ;(2)
;(2)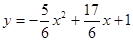 ;
;
(3)当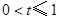 时,
时,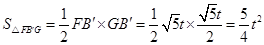
当 时,
时, 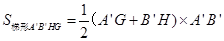
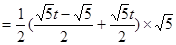
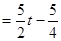 ;
;
当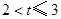 时,
时,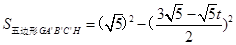 =
=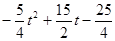 .
.
解析试题分析:(1)根据二次函数的性质及正方形的性质求解即可;
(2)设抛物线为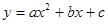 ,由抛物线过点
,由抛物线过点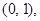
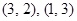 根据待定系数法求解即可;
根据待定系数法求解即可;
(3)分三种情况:当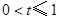 时,当
时,当 时,当
时,当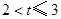 时,根据相似三角形的性质及对应多边形的面积公式求解即可.
时,根据相似三角形的性质及对应多边形的面积公式求解即可.
(1)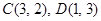 ;
;
(2)设抛物线为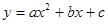 ,
,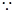 抛物线过点
抛物线过点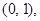
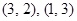 ,
,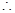
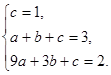 解得
解得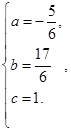
∴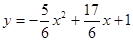 ;
;
(3)①当点A运动到点F时,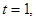
当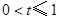 时,如图1,
时,如图1,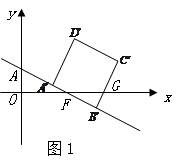
∵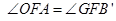 ,
,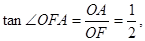
∴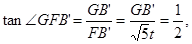
∴
∴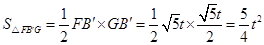 ;
;
②当点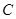 运动到
运动到 轴上时,
轴上时,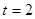 ,
,
当 时,如图2,
时,如图2, 
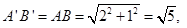
∴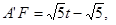
∴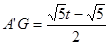 ,
,
∵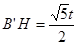 ,
,
∴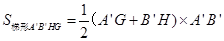
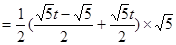
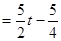 ;
;
③当点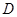 运动到
运动到 轴上时,
轴上时,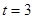 ,
,
当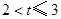 时,如图3,
时,如图3,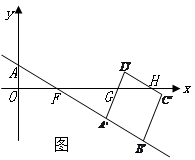
∵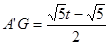 ,
,
∴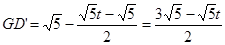
∵
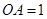 ,
,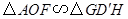
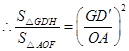 ,
,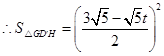 ,
,
∴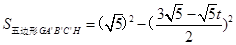 =
=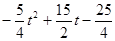 .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目

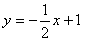 交坐标轴于
交坐标轴于 两点,以线段
两点,以线段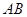 为边向上作正方形
为边向上作正方形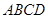 ,过点
,过点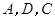 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为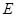 .
.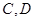 的坐标
的坐标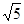 个单位长度的速度沿射线
个单位长度的速度沿射线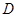 落在
落在 轴上时停止.设正方形落在
轴上时停止.设正方形落在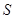 ,求
,求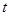 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量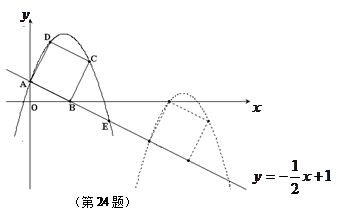
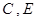 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.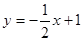 交坐标轴于
交坐标轴于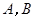 两点,以线段
两点,以线段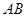 为边向上作正方形
为边向上作正方形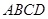 ,过点
,过点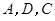 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为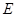 .
.
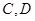 的坐标;
的坐标; 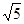 个单位长度的速度沿射线
个单位长度的速度沿射线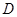 落在x轴上时停止.设正方形落在
落在x轴上时停止.设正方形落在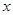 轴下方部分的面积为
轴下方部分的面积为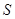 ,求
,求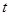 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量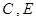 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.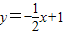 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.