Question

三条边长分别为2、3、8的等腰梯形的周长是________．

Answer 1

21
分析：在等腰梯形中作出一腰的平行线，将求梯形的周长问题转化为三角形的三边关系进行解答．
解答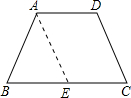：解：如图所示，
在等腰梯形ABCD中，过点A作腰CD的平行线，交BC于点E．
在等腰梯形ABCD中，
（1）若腰长AB=2，则AE=CD=AB=2，BE=BC-AD=8-3=5．
那么AB+AE=4＜BE=5．故不成立．
（2）若腰长AB=3，则AE=CD=AB=3，BE=BC-AD=8-2=6．
那么AB+AE=BE．故不成立．
（3）若腰长AB=8，则AE=CD=AB=8，BE=BC-AD=3-2=1．
符合三角形的两边之和大于第三边．
所以等腰梯形ABCD的周长=AB+BC+CD+AD=8+2+3+8=21．
故答案为：21．
点评：本题考查了解答梯形有关问题所作辅助线的方法、以及三角形的三边关系，有一定难度，注意细心讨论．