题目内容
如图，△OAB是边长为2的等边三角形，过点A的直线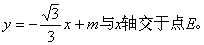
（1） 求点E的坐标；
（2） 求过 A、O、E三点的抛物线解析式；
（3） 若点P是（2）中求出的抛物线AE段上一动点（不与A、E重合），
设四边形OAPE的面积为S，求S的最大值。
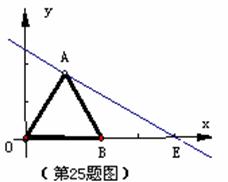
解：（1）作AF⊥x轴与F
∴OF=OAcos60°=1，AF=OFtan60°=
∴点A（1，）
代入直线解析式，得
，∴m=
∴
当y=0时，
得x=4， ∴点E（4，0）
（2）设过A、O、E三点抛物线的解析式为
∵抛物线过原点
∴c=0
∴
∴
∴抛物线的解析式为
…
（3）作PG⊥x轴于G，设
当
练习册系列答案
相关题目
S△ACD D.DE平分∠CDF
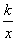(k>0)交于A，B两点，P是线段AB上的点(不与A，B重合)，过点A，B，P分别向x轴作垂线，垂足分别是C，D，E，连接OA，OB，OP，设△AOC面积是S1，△BOD面积是S2，△POE面积是S3，则( )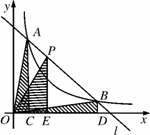
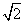≈1.4)
、0.2、
、
、
、
中，无理数的个数是__________． 