题目内容
4．
如图有一个棱长为9cm的正方体，一只蜜蜂要沿正方体的表面从顶点A爬到C点（C点在一条棱上，距离顶点B 3cm处），需爬行的最短路程是15cm．
分析 根据勾股定理求出AC即可．
解答 
解：∵CD=9cm，AD=（3+9）cm，
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15cm，
故答案为：15．
点评 本题考查了平面展开-最短路线问题和勾股定理的应用，主要考查学生的理解能力和计算能力．
练习册系列答案
相关题目
12．下列语句中，正确的有（ ）
（1）一条直角边和斜边上的高对应相等的两个直角三角形全等
（2）有两边和其中一边上的高对应相等的两个三角形全等
（3）有两边和第三边上的高对应相等的两个三角形全等．
（1）一条直角边和斜边上的高对应相等的两个直角三角形全等
（2）有两边和其中一边上的高对应相等的两个三角形全等
（3）有两边和第三边上的高对应相等的两个三角形全等．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．
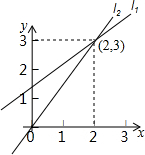如图，以两条直线l1，l2的交点坐标为解的方程组是（ ）
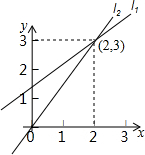如图，以两条直线l1，l2的交点坐标为解的方程组是（ ）| A． | $\left\{\begin{array}{l}3x-4y=6\\ 3x-2y=0\end{array}$ | B． | $\left\{\begin{array}{l}3x-4y=6\\ 3x+2y=0\end{array}$ | ||
| C． | $\left\{\begin{array}{l}3x-4y=-6\\ 3x-2y=0\end{array}$ | D． | $\left\{\begin{array}{l}-3x+4y=6\\ 3x+2y=0\end{array}$ |