题目内容
有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的存水量Q(升)随时间t(分)变化的函数关系.

(1)求线段BC所表示的Q与t之间的函数关系式,并写出自变量t的取值范围;
(2)现已知容器内有水200升,先打开两个进水管和一个出水管一段时间,然后再关上一个进水管,直至把容器放满水,若总共用时不超过8分钟。请问,在这个过程中同时打开两个进水管和一个出水管的时间至少是多少分钟?
【答案】
(1)-20x+600(5分 );(2)  分钟(
分钟(
【解析】
试题分析:由题意分析可知,B(0,600)C(30,0)
根据点线式可以求出该直线的解析式是y=-20x+600
(2)设时间是X,则满足200+10x- =8
=8
X=
考点:二次函数的综合题
点评:在解题时要能灵运用二次函数的图象和性质求出二次函数的解析式,利用数形结合思想解题是本题的关键

练习册系列答案
相关题目
 有一个装有进出水管的容器,每单位时间进出的水量都是一定的,设从某时刻开始的5分钟内只进水不出水,在随后的15分钟内既进水又出水,在前段过程中得到的时间x(分)与存水量y(升)之间的关系图象如图,若20分钟后只放水不进水,则这段时间内(x>20)y与x之间的函数关系式是( )
有一个装有进出水管的容器,每单位时间进出的水量都是一定的,设从某时刻开始的5分钟内只进水不出水,在随后的15分钟内既进水又出水,在前段过程中得到的时间x(分)与存水量y(升)之间的关系图象如图,若20分钟后只放水不进水,则这段时间内(x>20)y与x之间的函数关系式是( )| A、y=-2x+110(20<x≤55) | ||
| B、y=-2x-110(20<x≤55) | ||
C、y=-2x+95(20<x≤
| ||
| D、y=-2x+110(20<x≤50) |
 28、有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的容量Q(升)随时间t(分)变化的函数关系.
28、有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的容量Q(升)随时间t(分)变化的函数关系.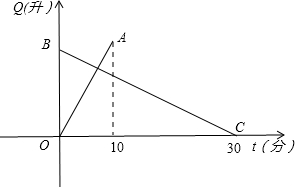
 开一个出水管时,容器内的水量Q(升)随时间t(分)变化的函数关系.根据图象进行以下探究:
开一个出水管时,容器内的水量Q(升)随时间t(分)变化的函数关系.根据图象进行以下探究: