题目内容
5.某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1m.(1)该车大灯照亮地面的宽度BC约是多少(不考虑其它因素)?
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,从60km/h到摩托车停止的刹车距离是$\frac{14}{3}$m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.参考数据:sin8°≈$\frac{7}{50}$,tan8°≈$\frac{1}{7}$,sin10°≈$\frac{4}{23}$,tan10°≈$\frac{5}{28}$.
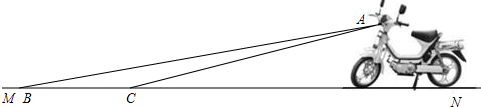
分析 (1)作AD⊥MN,垂足为D.在Rt△ADC中根据CD=$\frac{AD}{tan∠ACD}$求得CD的长;Rt△ABD中根据BD=$\frac{AD}{tan∠ABD}$求得BD的长,由BC=BD-CD可得;
(2)求出正常人作出反应过程中摩托车行驶的路程,加上刹车距离,然后与BD的长进行比较即可.
解答 解:(1)过A作AD⊥MN于点D,
在Rt△ACD中,∵∠ACD=10°,AD=1m,且tan∠ACD=$\frac{AD}{CD}$,
∴CD=$\frac{AD}{tan∠ACD}$=$\frac{1}{\frac{5}{28}}$=5.6(m),
在Rt△ABD中,∵∠ABD=8°,AD=1m,且tan∠ABD=$\frac{AD}{BD}$,
∴BD=$\frac{AD}{tan∠ABD}$=$\frac{1}{\frac{1}{7}}$=7(m),
∴BC=7-5.6=1.4(m).
答:该车大灯照亮地面的宽度BC是1.4m;
(2)该车大灯的设计不能满足最小安全距离的要求.理由如下:
∵以$60km/h=\frac{50}{3}m/s$的速度驾驶,最小安全距离为:$\frac{50}{3}×0.2+\frac{14}{3}=8$(m),
而大灯能照到的最远距离是BD=7m,
∴该车大灯的设计不能满足最小安全距离的要求.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
13.计算(-4)+(-9)的结果是( )
| A. | -13 | B. | -5 | C. | 5 | D. | 13 |
14.计算(-8)-(-5)的结果等于( )
| A. | -3 | B. | -13 | C. | -40 | D. | 3 |

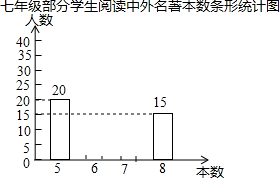 为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对该年级学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.
为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对该年级学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.