题目内容
11.把$\frac{\sqrt{45}}{2\sqrt{20}}$化成最简二次根式的结果是( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2$\sqrt{5}$ |
分析 根据同底数幂的除法,可得答案.
解答 解:原式=$\frac{1}{2}$×$\sqrt{\frac{45}{20}}$=$\frac{1}{2}$×$\sqrt{\frac{9}{4}}$=$\frac{3}{4}$,
故选:B.
点评 本题考查了最简二次根式,利用二次根式的除法、二次根式的性质是解题关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.随着旅游业的发展,2017年春节期间,我国出境游的人数约有610万人,数据610万用科学记数法表示为( )
| A. | 6.1×102 | B. | 610×104 | C. | 6.1×105 | D. | 6.1×106 |
19. 如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )
如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )
 如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )
如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
6.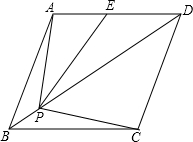 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
16.计算:($\frac{1}{1-x}$-$\frac{1}{x+1}$)÷$\frac{x}{x-1}$=( )
| A. | $\frac{2}{x+1}$ | B. | $\frac{2}{x-1}$ | C. | -$\frac{2}{x+1}$ | D. | -$\frac{2}{x-1}$ |
3.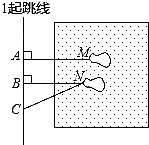 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )| A. | 线段AM | B. | 线段BN | C. | 线段CN | D. | 无法确定 |
1.若从多边形的一个顶点可以引出七条对角线,则这个多边形是( )
| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
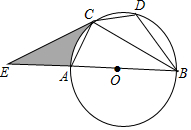 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC=CD,延长BA到E,连接EC,且∠ECA=∠CBD.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC=CD,延长BA到E,连接EC,且∠ECA=∠CBD.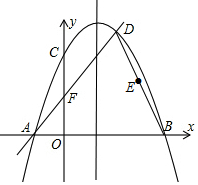 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).