题目内容
在小学,我们知道正方形具有性质“四条边都相等,四个内角都是直角”,请适当利用上述知识,解答下列问题:
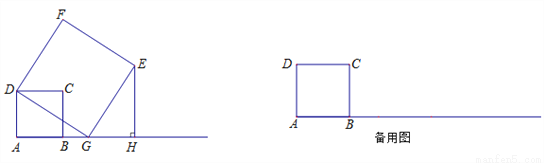
已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.
(1)填空:∠AGD+∠EGH= °;
(2)若点G在点B的右边.
①求证:△DAG≌△GHE;
②试探索:EH﹣BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
(3)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数;
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


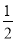 ,x﹣2,
,x﹣2, 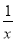 ,
, 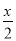 ,﹣
,﹣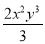 ,
, 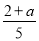 ,其中单项式有( )
,其中单项式有( )
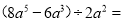 ___________.
___________.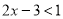 的解集在数轴上表示,正确的是( )
的解集在数轴上表示,正确的是( )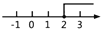 B.
B. 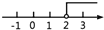 C.
C. 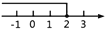 D.
D.