题目内容
某工厂每年的废气排放量为450万立方米,为加强环境保护,从2012年起,该厂决定经过设备改造等方式进行减排.
(1)若该厂要用五年的时间将废气排放量减至不高于250万立方米,那么每年平均至少要减少多少万立方米的废气排放量?
(2)2012、2013两年该厂的年废气排放量恰好均为五年平均值的最小值,2014年新的环境保护法出台后,该厂决定加大减排力度,决定用两年的时间刚好完成先前制定的减排计划.且2014年的减排量在2013年的基础上增加a%,2015年在2014年的基础上增加2a%,求a的值.(结果留根号)
(1)若该厂要用五年的时间将废气排放量减至不高于250万立方米,那么每年平均至少要减少多少万立方米的废气排放量?
(2)2012、2013两年该厂的年废气排放量恰好均为五年平均值的最小值,2014年新的环境保护法出台后,该厂决定加大减排力度,决定用两年的时间刚好完成先前制定的减排计划.且2014年的减排量在2013年的基础上增加a%,2015年在2014年的基础上增加2a%,求a的值.(结果留根号)
考点:一元二次方程的应用,一元一次不等式的应用
专题:计算题
分析:(1)设每年平均要减少x万立方米的废气排放量,根据用五年的时间将废气排放量减至不高于250万立方米列不等式,然后解不式即可;
(2)先利用(1)的结论得到2012、2013两年的年废气排放量,再表示出2014年和2015年的年废气排放量,然后根据2014年和2015年的年废气排放量的和列方程40(1+a%)+40(1+a%)(1+2a%)=200-40-40,然后解一元二次方程即可得到满足条件的a的值.
(2)先利用(1)的结论得到2012、2013两年的年废气排放量,再表示出2014年和2015年的年废气排放量,然后根据2014年和2015年的年废气排放量的和列方程40(1+a%)+40(1+a%)(1+2a%)=200-40-40,然后解一元二次方程即可得到满足条件的a的值.
解答:解:(1)设每年平均要减少x万立方米的废气排放量,
根据题意得450-5x≤250,
解得x≥40,
答:每年平均至少要减少40万立方米的废气排放量;
(2)根据题意得40(1+a%)+40(1+a%)(1+2a%)=200-40-40,
整理得a2+200a-5000=0,
解得a1=50
-100,a2=-50
-100(舍去).
所以a的值为50
-100.
根据题意得450-5x≤250,
解得x≥40,
答:每年平均至少要减少40万立方米的废气排放量;
(2)根据题意得40(1+a%)+40(1+a%)(1+2a%)=200-40-40,
整理得a2+200a-5000=0,
解得a1=50
| 6 |
| 6 |
所以a的值为50
| 6 |
点评:本题考查了一元二次方程的应用:列方程解决实际问题的一般步骤是:审清题意设未知数,列出方程,解所列方程求所列方程的解,检验和作答.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
关于抛物线y=x2-2x-3,下列说法错误的是( )
| A、其顶点坐标是(1,4) |
| B、与y轴的交点是(0,-3) |
| C、对称轴是直线x=1 |
| D、x轴的交点是(-1,0)和(3,0) |
小军从A地沿北偏西60°方向走10m到B地,再从B地向正南方向走20m到C地,此时小军离A地( )
A、5
| ||
| B、10m | ||
| C、15m | ||
D、10
|
若(x-4)(x+7)是二次三项式x2+ax-28的因式分解结果,那么a的值是( )
| A、3 | B、-3 | C、11 | D、-11 |
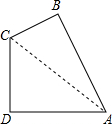 如图,在四边形ABCD中,∠B=∠D=90°,∠A:∠C=1:2,AB=2,CD=1,求:
如图,在四边形ABCD中,∠B=∠D=90°,∠A:∠C=1:2,AB=2,CD=1,求: