题目内容
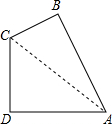 如图,在四边形ABCD中,∠B=∠D=90°,∠A:∠C=1:2,AB=2,CD=1,求:
如图,在四边形ABCD中,∠B=∠D=90°,∠A:∠C=1:2,AB=2,CD=1,求:(1)∠A、∠C的度数;
(2)AD、BC的长度.
考点:多边形内角与外角,勾股定理,矩形的判定与性质
专题:
分析:(1)由四边形内角和为360°及∠B=∠D=90°,得出∠A+∠C=180°,又∠A:∠C=1:2,即可求出∠A、∠C的度数;
(2)延长AD与BC,两延长线交于点E,由∠B=∠D=90°,得到三角形ABE与三角形CDE都为直角三角形,由∠A=60°,得到∠E=30°,在直角三角形CDE中,利用30°所对的直角边等于斜边的一半,根据CD的长求出DE的长,同理在直角三角形ABE中,由AB的长求出AE的长,用AE-DE求出AD的长,用BE-CE求出BC的长即可.
(2)延长AD与BC,两延长线交于点E,由∠B=∠D=90°,得到三角形ABE与三角形CDE都为直角三角形,由∠A=60°,得到∠E=30°,在直角三角形CDE中,利用30°所对的直角边等于斜边的一半,根据CD的长求出DE的长,同理在直角三角形ABE中,由AB的长求出AE的长,用AE-DE求出AD的长,用BE-CE求出BC的长即可.
解答:解:(1)在四边形ABCD中,∵∠B=∠D=90°,
∴∠A+∠C=180°,
又∠A:∠C=1:2,
∴∠A=60°,∠C=120°;
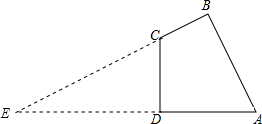 (2)延长AD与BC,两延长线交于点E,如图所示,
(2)延长AD与BC,两延长线交于点E,如图所示,
∵∠B=90°,∠A=60°,
∴∠E=30°,
在Rt△CDE中,CD=1,
∴CE=2CD=2,
根据勾股定理得:DE=
=
,
在Rt△ABE中,AB=2,
∴AE=2AB=4,
根据勾股定理得:BE=
=2
,
则AD=AE-DE=4-
,BC=BE-CE=2
-2.
∴∠A+∠C=180°,
又∠A:∠C=1:2,
∴∠A=60°,∠C=120°;
 (2)延长AD与BC,两延长线交于点E,如图所示,
(2)延长AD与BC,两延长线交于点E,如图所示,∵∠B=90°,∠A=60°,
∴∠E=30°,
在Rt△CDE中,CD=1,
∴CE=2CD=2,
根据勾股定理得:DE=
| CE2-CD2 |
| 3 |
在Rt△ABE中,AB=2,
∴AE=2AB=4,
根据勾股定理得:BE=
| AE2-AB2 |
| 3 |
则AD=AE-DE=4-
| 3 |
| 3 |
点评:此题主要考查了勾股定理,含30°角的直角三角形的性质,四边形内角和定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
AB为直线跑道,甲、乙二人同时从A出发,往返匀速跑步,v甲:v乙<2.当甲第4次回到A时,乙还没有跑够3个来回,并且在距离B尚有全程三分之一路程的位置向A跑来.当甲在B时,乙的所有可能位置是( )
A、B和距离B尚有
| ||
B、A和距离A尚有
| ||
C、B和距离A尚有
| ||
D、A和距离B尚有
|